因子分析とは
因子分析には以下の2種類がある。
- 探索的因子分析(exploratory FA, EFA):何も仮説を考えないまま、データの背景にありそうな因子構造を推定するもの
- 検証的因子分析(confirmatory FA, CFA):先行する理論をもとに因子・観察変数の関係性をあらかじめ設定して、データがその因子構造に当てはまるのかを検証するもの。確認的因子分析とも呼ばれる。
検証的因子分析の手順
- データの確認
- 因子構造の指定
- モデルの当てはめ
- 推定結果の確認
- モデルの改善
使用するパッケージとデータセット
CFAは主にlavaan*1パッケージを使うが、他に関連するパッケージもまとめて読み込んでおく。
- lavaanパッケージ:Latent variable analysis = 潜在変数を扱う解析、つまりCFAや構造方程式モデリング(Structural Equation Modeling, SEM)を行える
- MVNパッケージ:正規性(後述)の確認
- semToolsパッケージ:信頼性(後述)の確認
- semPlot:パス図を描く
library(lavaan) library(MVN) library(semTools) library(semPlot)
lavaanパッケージのHolzingerSwineford1939データセットを用いる。
> head(HolzingerSwineford1939) id sex ageyr agemo school grade x1 x2 x3 x4 x5 x6 x7 x8 x9 1 1 1 13 1 Pasteur 7 3.333333 7.75 0.375 2.333333 5.75 1.2857143 3.391304 5.75 6.361111 2 2 2 13 7 Pasteur 7 5.333333 5.25 2.125 1.666667 3.00 1.2857143 3.782609 6.25 7.916667 3 3 2 13 1 Pasteur 7 4.500000 5.25 1.875 1.000000 1.75 0.4285714 3.260870 3.90 4.416667 4 4 1 13 2 Pasteur 7 5.333333 7.75 3.000 2.666667 4.50 2.4285714 3.000000 5.30 4.861111 5 5 2 12 2 Pasteur 7 4.833333 4.75 0.875 2.666667 4.00 2.5714286 3.695652 6.30 5.916667 6 6 2 14 1 Pasteur 7 5.333333 5.00 2.250 1.000000 3.00 0.8571429 4.347826 6.65 7.500000
含まれる変数は以下のとおり。
id:IDsex:性別ageyr:年齢の年の部分agemo:年齢の月の部分school:児童の所属する学校grade:学年x1:visual perception(視覚)x2:cubes(立方体?)x3:lozenges(菱形?)x4:paragraph comprehension(パラグラフ理解)x5:sentence completion(文章補完)x6:word meaning(語彙)x7:speeded addition(速く足す)x8:speeded counting of dots(速く数える)x9:speeded discrimination straight and curved capitals(速く区別する)
x1〜x9だけ使う。
data <- HolzingerSwineford1939[-c(1:6)]
1. データの確認
まずはデータ(観察変数)の正規性を確認する。MVNパッケージのmvn( )で一気に確認できる。
> mvn(data) $multivariateNormality Test Statistic p value Result 1 Mardia Skewness 344.905276936947 8.86473544030093e-15 NO 2 Mardia Kurtosis 2.83021589156651 0.00465166039260279 NO 3 MVN <NA> <NA> NO $univariateNormality Test Variable Statistic p value Normality 1 Shapiro-Wilk x1 0.9928 0.1582 YES 2 Shapiro-Wilk x2 0.9697 <0.001 NO 3 Shapiro-Wilk x3 0.9523 <0.001 NO ~~~~~(省略)~~~~~ $Descriptives n Mean Std.Dev Median Min Max 25th 75th Skew Kurtosis x1 301 4.935770 1.167432 5.000000 0.6666667 8.500000 4.166667 5.666667 -0.2543455 0.30753382 x2 301 6.088040 1.177451 6.000000 2.2500000 9.250000 5.250000 6.750000 0.4700766 0.33239397 x3 301 2.250415 1.130979 2.125000 0.2500000 4.500000 1.375000 3.125000 0.3834294 -0.90752645 ~~~~~(省略)~~~~~
$multivariateNormalityで多変量正規分布と見なせるかどうかを検定している。結果は"NO"なので正規分布とは見なせない。
多変量正規分布と見なせるならば最尤法を使うが、見なせないならロバスト最尤法を用いる。推定方法は、モデルの当てはめのときに指定する。
2. 因子構造の指定
モデル式を書いて因子構造を指定する。SEMで指定するような複雑なモデルを記述できるように構文が用意されている。4種類の式のタイプがあるみたいですが、詳細はまた勉強します。
=~:潜在変数の定義~:回帰~~:残差の分散・共分散y ~ 1:切片
ここでは3つの潜在因子F1〜F3に対して、観察変数を以下のように割り当てた。
model = " F1 =~ x1 + x2 + x3 F2 =~ x4 + x5 + x6 F3 =~ x7 + x8 + x9 "
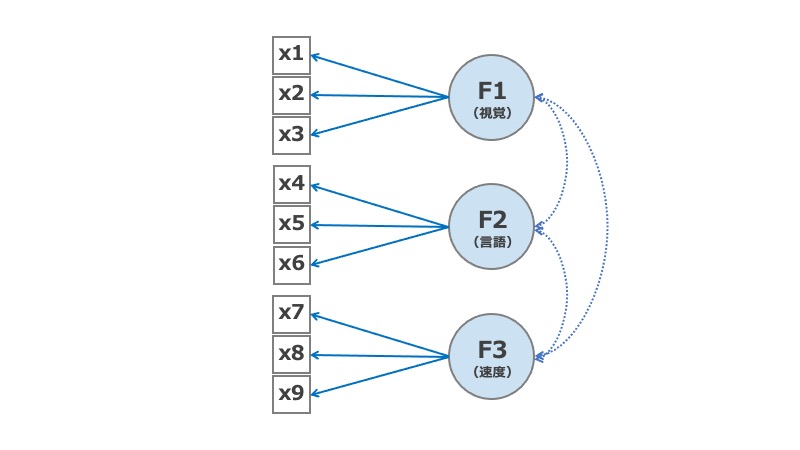
ちなみに因子間に独立を想定する場合は、以下のようにすると因子間相関係数=0になる。
model = " F1 =~ x1 + x2 + x3 F2 =~ x4 + x5 + x6 F3 =~ x7 + x8 + x9 F1 ~~ 0*F2 F1 ~~ 0*F3 F2 ~~ 0*F3 "
さらに、
model = " F1 =~ x1 + x2 + x3 F2 =~ x4 + x5 + x6 F3 =~ x7 + x8 + x9 F1 ~~ 1*F1 F2 ~~ 1*F2 F3 ~~ 1*F3 "
とすると、各因子の分散を1に固定する(cfa( )でstd.lv = TRUEを指定するのと同じだと思う)。
3. モデルの当てはめ
モデル式とデータをcfa( )に渡して、因子負荷や相関を推定する。 指定する主な引数は、
estimator:推定方法。最尤法なら"ML"、ロバスト最尤法なら"MLR"を指定。デフォルトは"ML"みたい。std.lv:TRUEを指定すると因子分散が1となるように標準化される。TRUEを指定しないとデフォルトのauto.fix.first = TRUEが指定され、各因子の中で1つ目に指定した変数のパラメータが1に固定される。因子分散を1に固定すると因子のバラツキ具合について比較できないが、1に固定して表示するのが普通なのかな。
fit <- cfa(model = model, data = data, estimator = "MLR", std.lv = TRUE)
4. 推定結果の確認
結果は以下のコードで表示。
fit.measures:適合度指標を表示したいときはTRUEにするstandardized:結果でStd.lvとStd.allを表示したいときはTRUEにする。
summary(fit, fit.measures=FALSE, standardized=TRUE)
結果は長いので分割しながら見ていく。
4-1. 推定の概要
使用されたlavaanのバージョン、収束までの回数、パラメータ数、観測数などが表示される。
lavaan 0.6-8 ended normally after 20 iterations Estimator ML Optimization method NLMINB Number of model parameters 21 Number of observations 301
"ended normally"とあるので、ここでは推定は正常に収束したみたい。
4-2. モデルの適合度
ここではRobustの方を見る。
Model Test User Model: Standard Robust Test Statistic 85.306 87.132 Degrees of freedom 24 24 P-value (Chi-square) 0.000 0.000 # Scaling correction factor 0.979 Yuan-Bentler correction (Mplus variant) Model Test Baseline Model: Test statistic 918.852 880.082 Degrees of freedom 36 36 P-value 0.000 0.000 Scaling correction factor 1.044 User Model versus Baseline Model: Comparative Fit Index (CFI) 0.931 0.925 # Tucker-Lewis Index (TLI) 0.896 0.888 # Robust Comparative Fit Index (CFI) 0.930 # Robust Tucker-Lewis Index (TLI) 0.895 # Loglikelihood and Information Criteria: Loglikelihood user model (H0) -3737.745 -3737.745 Scaling correction factor 1.133 for the MLR correction Loglikelihood unrestricted model (H1) -3695.092 -3695.092 Scaling correction factor 1.051 for the MLR correction Akaike (AIC) 7517.490 7517.490 Bayesian (BIC) 7595.339 7595.339 Sample-size adjusted Bayesian (BIC) 7528.739 7528.739 Root Mean Square Error of Approximation: RMSEA 0.092 0.093 # 90 Percent confidence interval - lower 0.071 0.073 90 Percent confidence interval - upper 0.114 0.115 P-value RMSEA <= 0.05 0.001 0.001 Robust RMSEA 0.092 # 90 Percent confidence interval - lower 0.072 90 Percent confidence interval - upper 0.114 Standardized Root Mean Square Residual: SRMR 0.065 0.065 #
P-value (Chi-square):最尤統計量から得たカイ2乗分布に基づくP値。Model Test User Modelのところを見る。>0.05ならOKと言われるが、サンプルサイズが大きいと感度が良すぎる(75-200がちょうどよく、400以上ではいつも有意になってしまう*2)。この「感度が良すぎる問題」があるので、普通は以下の指標が使われる。- 相対的な適合との指標:ベースラインモデル(最も簡単なモデル)との相対的な比較を行う。
Model Test User ModelとModel Test Baseline Modelの情報を使っている。Comparative Fit Index (CFI):0〜1の値を取る。大きいほど良い。>0.95(甘くしても>0.9)ならOK。多分ここでもRobust CFIの方を見るのかな、と。Tucker-Lewis Index (TLI):0〜1の値を取る(1以上になるときは1に丸める)。>0.90なら適合度OK。
- 絶対的な適合度の指標:
SRMR:Standard root mean squareで、≦0.08ならOKRMSEA:root mean square error of approximationの略。RMSEAが大きいほど、適合度が悪い。≦0.05ならぴったり適合、≧0.10なら適合良くない。ロバスト最尤法を使ったのなら、Robustの方を見るのかな。
4-3. 推定値
Parameter Estimates: Standard errors Sandwich Information bread Observed Observed information based on Hessian Latent Variables: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 =~ x1 0.900 0.100 8.973 0.000 0.900 0.772 x2 0.498 0.088 5.681 0.000 0.498 0.424 x3 0.656 0.080 8.151 0.000 0.656 0.581 F2 =~ x4 0.990 0.061 16.150 0.000 0.990 0.852 x5 1.102 0.055 20.146 0.000 1.102 0.855 x6 0.917 0.058 15.767 0.000 0.917 0.838 F3 =~ x7 0.619 0.086 7.193 0.000 0.619 0.570 x8 0.731 0.093 7.875 0.000 0.731 0.723 x9 0.670 0.099 6.761 0.000 0.670 0.665 Covariances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 ~~ F2 0.459 0.073 6.258 0.000 0.459 0.459 F3 0.471 0.119 3.954 0.000 0.471 0.471 F2 ~~ F3 0.283 0.085 3.311 0.001 0.283 0.283 Variances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all .x1 0.549 0.156 3.509 0.000 0.549 0.404 .x2 1.134 0.112 10.135 0.000 1.134 0.821 .x3 0.844 0.100 8.419 0.000 0.844 0.662 .x4 0.371 0.050 7.382 0.000 0.371 0.275 .x5 0.446 0.057 7.870 0.000 0.446 0.269 .x6 0.356 0.047 7.658 0.000 0.356 0.298 .x7 0.799 0.097 8.222 0.000 0.799 0.676 .x8 0.488 0.120 4.080 0.000 0.488 0.477 .x9 0.566 0.119 4.768 0.000 0.566 0.558 F1 1.000 1.000 1.000 F2 1.000 1.000 1.000 F3 1.000 1.000 1.000
Std.lvは潜在変数だけが標準化されていて、Std.allは潜在変数と観測変数の両方が標準化されている。
因子負荷量(factor loading, FL)
Latent VariableのStd.allを見る- FLは0〜1の範囲に収まっているはずで、>1の場合はHeywood caseと呼ばれる*3
0.5なら意味のある関連と考えていい
- 全ての因子負荷量のP値は統計学的に有意でなくてはならない。
因子間相関(factor correlation)
CovariancesのStd.allを見る- <0.85であれば因子が明確に区別されていることを示す。反対に>0.85だと多重共線性の問題ありかも。
因子分散および独自因子の分散
VariancesのEstimateを見る- ここでは因子分散を1に固定しているので上記の結果。
4-4. パス図を描く
semPlotパッケージのsemPaths( )を使ってパス図を描く。
第1引数はcfa( )で作成したオブジェクト。その後、"path", "std"を指定。前者だけだと矢印しか描かれない。
styleは分散を表現するときに、双頭矢印(両方とも同じノードに向かう)なら"ram", "mx", "OpenMx"、一方向矢印なら"lisrel"を指定する。
デフォルトだと矢印の色がグレーなので、黒にしたいときはedge.colorで指定。
semPaths(fit, "path", "std", style = "lisrel", edge.color = "black", intercepts = FALSE)
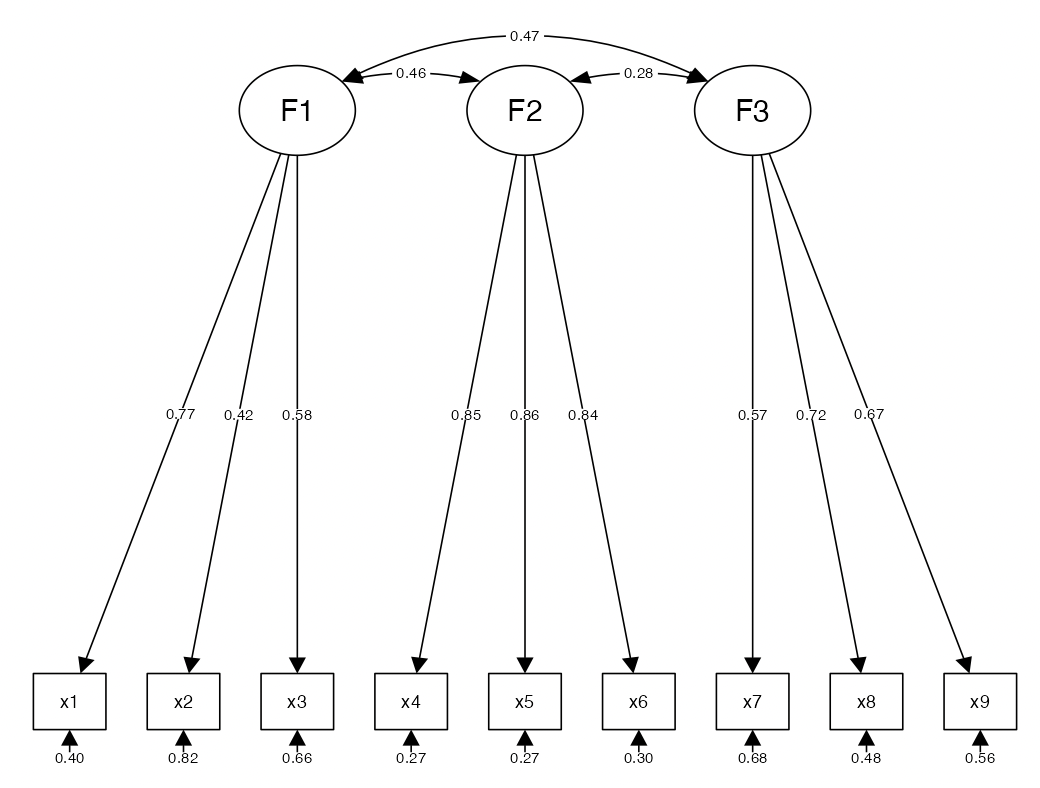
先程のパラメータ推定値のStd.allが書き込まれていることを確認。
5. モデルの改善
5-1. 当てはまりの悪い部分を探す
モデルの当てはまりが悪かった場合、どこを変えたらいいのかを見るために、当てはまりの悪い部分を探す。
1つ目はmodification index(MI)で、>3.84を超えるところは改善の余地ありと判断。
> mis_fit <- modificationIndices(fit) > subset(mis_fit, mi>3.84) lhs op rhs mi epc sepc.lv sepc.all sepc.nox 10 F1 ~~ F2 26.552 0.388 0.388 0.388 0.388 11 F1 ~~ F3 22.633 0.393 0.393 0.393 0.393 12 F2 ~~ F3 12.152 0.248 0.248 0.248 0.248 25 F1 =~ x4 4.653 0.112 0.112 0.097 0.097 27 F1 =~ x6 9.912 0.157 0.157 0.144 0.144 28 F1 =~ x7 4.725 -0.145 -0.145 -0.133 -0.133 30 F1 =~ x9 40.044 0.399 0.399 0.396 0.396 31 F2 =~ x1 31.475 0.354 0.354 0.304 0.304 36 F2 =~ x9 10.298 0.175 0.175 0.173 0.173 37 F3 =~ x1 10.504 0.224 0.224 0.192 0.192 39 F3 =~ x3 4.612 0.142 0.142 0.125 0.125 45 x1 ~~ x4 6.547 0.111 0.111 0.197 0.197 50 x1 ~~ x9 14.396 0.200 0.200 0.263 0.263 55 x2 ~~ x7 6.279 -0.148 -0.148 -0.166 -0.166 59 x3 ~~ x5 4.487 -0.095 -0.095 -0.186 -0.186 63 x3 ~~ x9 4.651 0.109 0.109 0.164 0.164 66 x4 ~~ x7 7.095 0.106 0.106 0.198 0.198
もう1つはstandardized residuals(SR)で、|SR|>2.58は改善の余地ありと判断。
> sr <- residuals(fit, type = "standardized") > sr $type [1] "standardized" $cov x1 x2 x3 x4 x5 x6 x7 x8 x9 x1 0.000 x2 0.000 0.000 x3 0.000 0.000 0.000 x4 5.497 2.517 2.784 0.000 x5 4.688 2.394 1.309 0.000 0.000 x6 5.119 2.996 3.126 0.000 0.000 0.000 x7 1.084 -1.430 1.247 2.928 1.662 2.031 0.000 x8 3.531 1.682 3.081 1.798 2.228 2.358 0.000 0.000 x9 6.325 3.613 5.462 3.138 3.849 3.025 0.000 0.000 0.000
5-2. 因子の信頼性を評価する
semToolsパッケージのreliablity( )でRaykov’s rhoを計算する。
> rel <- reliability(fit) > print(rel, digits = 3) F1 F2 F3 alpha 0.626 0.883 0.688 omega 0.633 0.886 0.696 omega2 0.633 0.886 0.696 omega3 0.633 0.886 0.696 avevar 0.369 0.723 0.438
omegaがRaykov’s rhoに相当。≧0.70なら信頼性あり。
alphaはCronbachのα係数。
おわりに
- モデル式を使ってパラメータとか分散を自在に固定できるようになるには、まだまだ訓練が必要だが...私には使う機会がなさそう。
- しばらくウェットの餌が続くと、ドライを出したときに「これじゃないでしょ?」って顔で見てきます。
参考資料
- lavaanパッケージのチュートリアルです。
- 適合度指標の計算方法については、以下の資料を参考にしました。
*1:Latent Variable Analysis