空間データを可視化する(2)（sfパッケージ） [R]

はじめに

Rのsfパッケージを使って、神戸市の校区境界と学校所在地をプロットしようとしています。前回はデータのダウンロードから加工（部分抽出・変数追加）までやってみました。

necostat.hatenablog.jp

今回はプロットしてみます。

GISデータをプロットしてみる

例1：plot( )を使う

まずは中学校区を標準のplot( )を使ってみます。

plot(MS_poly_kobe)

各属性データにもとづいて塗り分けられた図が作成されました。

3番目の図だけ欲しかったら、

plot(MS_poly_kobe[3])

とします（出力は割愛）。

例2：geom_sf( )を使う

ggplot2での作図に慣れている人は、geom_sf( )を使うと便利です。

ggplot() +
  geom_sf(data = ES_poly_kobe) +
  theme_minimal()

例3：離散変数に従って塗り分ける

3つのカテゴリーをランダムに割り当てた離散変数に従って、小学校区を塗り分けてみます。 面を塗る色を指定する引数はfill、境界線の色を指定する引数はcolourです。

ggplot() +
  geom_sf(data = ES_poly_kobe, aes(fill = rnd_cat), colour = "white") +
  theme_minimal() 

例4：連続変数に従って塗り分ける

次はランダムに作成した連続変数に従って塗り分けてみます。

ggplot() +
  geom_sf(data = ES_poly_kobe, aes(fill = rnd_cont)) +
  scale_fill_gradient(low = "#FFFFFF", high = "#336699") +
  theme_minimal()

例5：複数の図を重ねる

geom_sf( )を使えば、複数の図を重ねることも簡単です。 中学校区境界の白地図に、中学校所在地を重ねてみましょう。 所在地のプロットの色は連続カラースケールにしてみます。

ggplot() +
  geom_sf(data = MS_poly_kobe, fill = "white") +
  geom_sf(data = MS_point_kobe, aes(colour = rnd_cont)) +
  scale_colour_gradient(low = "#FF6B6B", high = "#336699") +
  theme_minimal()

レイヤーの順序を入れ替えるときは注意が必要です。面データを後から重ねるときは、下のように透過度100%（alpha=0）にしておかないと、先にプロットした所在地が見えなくなってしまいます。

ggplot() +
  geom_sf(data = MS_point_kobe, aes(colour = rnd_cont)) +
  geom_sf(data = MS_poly_kobe, alpha = 0) +
  scale_colour_gradient(low = "#FF6B6B", high = "#336699") +
  theme_minimal()

出力は省略します。

おわりに

• 元々の属性にある「学校名」などに従って塗り分けるときは、凡例を表示しないようにしておく方がいいです。

ggplot() +
  geom_sf(data = ES_poly_kobe, aes(fill = A27_004), alpha = 0.5) +
  theme_minimal() + 
  theme(legend.position = "none")

• 久しぶりの投稿ですが、猫2匹は元気にしています。

参考資料

• GISデータに関する基礎的な解説がわかりやすいです。

www.esrij.com

空間データを可視化する(1)（sfパッケージ） [R]

はじめに

例えば、人口密度などの特性によって都道府県を塗り分けた図や、医療機関の位置を地図上にプロットした図など、地理空間情報を含んだデータをグラフにしたものを見る機会は多いですよね。 最近はExcelでも簡単に作成できるみたいです（ マップ グラフを作成する Excel - Microsoft サポート ）

Rを使う方が痒い所に手が届くと思うので、今回はRのsfパッケージを使って、神戸市の校区境界と学校所在地をプロットしてみます。

GISデータを準備する

GISとは Geographic Information System の略で、地理情報システムと訳されます。いくつかの機関がGISデータを無償で提供してくれています。 地図と聞いて真っ先に浮かぶ国土地理院もGISデータを無償提供していますが、今回は提供しているデータの種類が豊富な国土数値情報（提供：国土交通省 国土政策局）を使います。

nlftp.mlit.go.jp

今回は以下のzipファイルをダウンロードして使ってみました。

• 兵庫県の中学校区（2021年）：A32-21_28_GML.zip
• 兵庫県の小学校区（2021年）：A27-21_28_GML.zip
• 兵庫県の学校所在地（2021年）P29-21_28_GML.zip

データファイルの概要

GISデータは、位置や区域を表す形状データと、その点・区域の特徴を示す属性データから構成されます。形状データは以下の4種類があります。

• 点データ：建物の位置
• 線データ：河川や道路の形を表す線分データ
• 面データ：行政や校区の境界を表す多角形データ（ポリゴン*1データともいう）
• メッシュデータ：エリアを格子状に区切ったデータ（ラスタデータ*2ともいう）

ダウンロードされた圧縮ファイルを解凍して得られるフォルダの中には、いくつかファイルが入っています。必須のファイルは以下の3つです。

• .shp：主に形状データを格納しているファイル
• .shx：データの検索効率を向上するためのインデックス情報を格納するファイル
• .dbf：属性データを格納しているファイル

データの読み込みと確認

まず必要なパッケージを読み込みます。

library(sf)
library(tidyverse)

次に、read_sf( )を使って.shpファイルを読み込みます。他の2つの必須ファイル（.shx, .dbf）も同じ場所に置いておきます。

MS_poly <- read_sf("A32-21_28.shp") # 中学校区境界
ES_poly <- read_sf("A27-21_28.shp") # 小学校区境界
S_point <- read_sf("P29-21_28.shp") # 学校所在地

glimpse( )で中学校区データ（A32-21_28.shp）の構造の概要を確認します。

> MS_poly %>% glimpse()
Rows: 287
Columns: 6
$ A32_001  <chr> "28100", "28100", "28100", "28100", "28100", "28100", "28100", "28100"…
$ A32_002  <chr> "神戸市", "神戸市", "神戸市", "神戸市", "神戸市", "神戸市", "神戸市", …
$ A32_003  <chr> "C128210000514", "C128210000373", "C128210000104", "C128210000337", "C…
$ A32_004  <chr> "伊川谷中学校", "井吹台中学校", "烏帽子中学校", "雲雀丘中学校", "塩屋…
$ A32_005  <chr> "神戸市西区伊川谷町上脇字鬼神山1005-2", "神戸市西区井吹台西町2-3", "神…
$ geometry <MULTIPOLYGON [°]> MULTIPOLYGON (((135.0291 34..., MULTIPOLYGON (((135.0296 …

ここでgeometryは形状データで、"MULTIPOLYGON"とあるので多角形データとわかります。 他の5つは属性データです。どの変数がどんな属性を表しているかは、国土数値情報のダウンロードサイトに書いてあります。

• A32_001：中学校が存在する行政区域コード*3
• A32_002：設置主体
• A32_003：学校に設定された固有の学校コード
• A32_004：学校の名称
• A32_005：学校の所在地住所

小学校区データ（A27-21_28.shp）に保存されている属性も同じ内容ですが、変数名が異なります（例：A27_001）。

学校所在地データ（P29-21_28.shp）についても見てみます。

> S_point %>% glimpse()
Rows: 2,622
Columns: 8
$ P29_001  <chr> "28203", "28228", "28207", "28100", "28100", "28100", "28100", "28100"…
$ P29_002  <chr> "A128110000011", "A128110000020", "A128210000019", "A128210000028", "A…
$ P29_003  <int> 16011, 16011, 16011, 16011, 16011, 16011, 16011, 16011, 16011, 16011, …
$ P29_004  <chr> "神戸大学附属幼稚園", "兵庫教育大学附属幼稚園", "伊丹幼稚園ありおか分…
$ P29_005  <chr> "明石市山下町3-4", "加東市山国2013-4", "伊丹市伊丹7-1-30", "神戸市東灘…
$ P29_006  <int> 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3…
$ P29_007  <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ geometry <POINT [°]> POINT (134.9986 34.64958), POINT (134.9808 34.91444), POINT (135…

今度は形状データが"POINT"、つまり点データになっていますね。属性は以下のとおりです。

• P29_001：行政区域コード
• P29_002：学校コード
• P29_003：学校分類（16001=小学校、16002=中学校など）
• P29_004：学校の名称
• P29_005：学校の所在地
• P29_006：管理者コード（1=国、2=都道府県、3=市区町村、4=民間、0=その他）
• P29_007：休校区分（0=調査なし、1=開校中、2=休校中）

データの一部を抽出する

今回は神戸市だけプロットするので、兵庫県全体の中から該当する部分を抽出してきます。行政区域コードや設置主体で条件を設定します。

MS_poly_kobe <- MS_poly %>% 
  filter(A32_001 %in% c("28100", "28101", "28102", "28105", "28106", "28107", "28109", "28110", "28111"))

ES_poly_kobe <- ES_poly %>% 
  filter(A27_001 %in% c("28100", "28101", "28102", "28105", "28106", "28107", "28109", "28110", "28111"))

各データの説明ページにあるリンクから行政区域コード一覧が収められたExcelファイルを入手できます。

ここから、28100（神戸市）, 28101（神戸市東灘区）, ... , 28111（神戸市西区）を選んで指定しました。

学校所在地データについては、以下のコードで神戸市内の公立中学校のみ抽出しました。

MS_point_kobe <- S_point %>% 
  filter(P29_001 %in% c("28100", "28101", "28102", "28105", "28106", "28107", "28109", "28110", "28111")) %>% 
  filter(P29_003 %in% c(16002,16003, 16014)) %>% 
  filter(P29_006 == 3) %>%
  filter(P29_007 == 1)

指定した条件は以下のとおりです。

• 行政区域コード（P29_001）：前述のとおり
• 学校分類コード（P29_003）：16002=中学校, 16003=中等教育学校*4, 16014=義務教育学校*5
• 管理者コード（P29_006）：3=市区町村
• 休校区分（P29_007）：1=開校中

属性データを付け加える

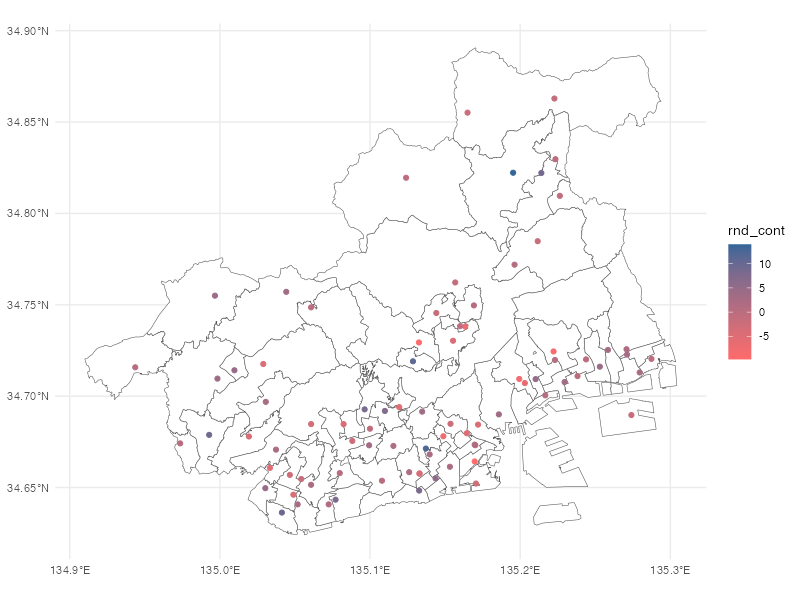
提供されている属性以外の情報を加えて、地図を塗り分けたいということがあると思います。ここではランダムなカテゴリー変数（rnd_cat）とランダムな連続変数（rnd_cont）を追加しておいて、後で塗り分けに使いたいと思います。

set.seed(1234)

ES_poly_kobe <- ES_poly_kobe %>% 
  rowwise() %>% 
  mutate(rnd_cat = sample(c("A","B","C"),prob=c(0.2,0.3,0.5),size=1,replace=TRUE)) %>% 
  mutate(rnd_cont = rnorm(n=1,mean=0,sd=5))

MS_point_kobe <- MS_point_kobe %>% 
  rowwise() %>% 
  mutate(rnd_cat = sample(c("A","B","C"),prob=c(0.2,0.3,0.5),size=1,replace=TRUE)) %>% 
  mutate(rnd_cont = rnorm(n=1,mean=0,sd=5))

おわりに

• 中学校区数79、中学校数84と乖離がありました。設置主体で条件付けても同じでした。一部は分校によるものでしたが、それ以外にも統廃合などの影響がありそうです。
• 次回は実際にプロットしてみます。

参考資料

• GISデータに関する基礎的な解説がわかりやすいです。

www.esrij.com

*1:「多角形」という意味

*2:線・面のように点を繋いで形状を表したものをベクタデータという

*3:都道府県コードと市区町村コードを組み合わせて定義されている

*4:中高一貫なので多分私立のみだが念のため

*5:小中一貫

高校生のためのデータ分析入門 (30)：解析環境を準備しよう！

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書いてきました。30回目の今回で一区切り、シーズン終了（修了）です。前回に引き続き、最終回も実際にデータを分析する準備をしていきましょう。

クラウドサービスを使えば解析環境を簡単に導入できる！

最近は高校生でも1人1台パソコンを持たされるところも多いようです。すごい時代になりました。 しかし、ソフト（=アプリ）を入れるとなると制限がかかってしまい、完全に自由に使えるわけではなさそうですね。 そんな人のために、知っておくと便利なクラウドサービスを紹介したいと思います。

ちなみにクラウドサービスというのは、自分のパソコン上でソフトウェアが動くのではなく、オンライン上で色々やってくれるもの。Google Chrome, Edge, Safariといったブラウザで操作できますが、インターネットへの接続が必要です。

Google（グーグル）

Spreadsheet（スプレッドシート）

これは学校でも使ったことあるかもしれません。緑色の表計算アプリです。主にデータテーブルを作成する目的で使います（作成の仕方は前回記事を参照）。

スプレッドシートはあくまで表計算アプリなので、高度な統計解析はできませんが、関数を使って簡単な計算を実行することができます。 下に挙げるものは使う機会が多いので、確認しておくといいかもしれません。

• SUM：指定したセルの合計を返す
• AVERAGE：指定したセルの平均値を返す
• COUNT：指定したセルの個数を返す
• COUNTIF：指定した条件に該当するセルの個数を返す
• IF：条件に応じた値を返す

作成したデータシートは、後で紹介する解析環境に直接読み込むこともできますが、まずは一旦パソコンにファイルとしてダウンロードする方がいいです。そのときはcsv形式*1を選びましょう（下）。

Colaboratory（コラボラトリー）

これを使えば、現在最も人気のあるPython（パイソン）というプログラミング言語を実行することができます。 Pythonとして習っているのかどうか知りませんが、「情報」の教科書に登場するプログラムはPythonをもとにしているようですね。

Pythonはデータ分析だけでなく、色々な用途で使われているので、プログラミングを勉強したいと思ったら、まずPythonから始めるといいでしょう。近年、機械学習・深層学習（ディープラーニング）の注目度が高くなっていることもあり、とても人気のある言語です。

使い方は簡単です（プログラミングが簡単という意味ではない）。下のようにGoogleドライブで新規ファイルを作成するだけで始められます。

Colabファイルを開くとしたのような画面が出てきます。この箱（セル）の中にPythonのコード（プログラムを動かすための文章）を書いていきます。

試しに下のコード（作：Chat GPT）をコピペして実行してみてください。セルの左端の▶️を押せば実行できます。

import matplotlib.pyplot as plt
import numpy as np

# サンプルデータの生成
np.random.seed(0) # 乱数のシードを設定
x = np.random.rand(50) * 100  # 0から100までの乱数を50個生成
y = x * 2 + np.random.normal(0, 10, 50)  # xに対して線形の関係とランダムなノイズを加えたデータを生成

# 散布図の描画
plt.scatter(x, y)
plt.title('Sample Scatter Plot')  # タイトル
plt.xlabel('X')  # X軸のラベル
plt.ylabel('Y')  # Y軸のラベル
plt.grid(True)  # グリッドの表示
plt.show()

上のグラフが描けましたか？「コードで動かす」というと難しく聞こえますが、他の人やChat GPTが考えてくれたコードを利用できるので、とても便利です。

Posit Cloud（ポジットクラウド）

こちらは以前はRStudio Cloudと呼ばれていたもので、統計解析に特化したプログラミング言語であるR（アール）を実行することができます。

まずは下のリンクにアクセスしてください。

posit.cloud

下の画面が表示されると思います。「GET STARTED」と書かれたボタンを押します。

すると下のようなプランを選ぶ画面になります。1番左の無料プランを選んでください。

下の画面になるので、$0と書かれているのを確認してから「SIGN UP」を押します。

次に下のようなアカウント作成画面が出てきます。Googleのアカウントでサインインすることもできますが、学校から供与されているGoogleアカウントで入ろうとすると学校側がPosit Cloudの利用を承認する必要があります（ひょっとしてメールアドレスを使っても学校の端末からはアクセスできないかもしれません。自分のタブレットがあればいいんですが。スマホだとちょっと画面が小さすぎ…。）

アカウントを作成してログインすると、下のような画面が現れるので、右上の「New Project」から「New RStudio Project」を選びます。ちなみに、その下にある「Jupyter」はPythonを実行するためのものですが、無料版では使えないみたい。

Posit Cloudが起動したら、左上の「緑プラスボタン」から「R Script」を選んで押します。

この時点で、下のように4つの区画が表示されていると思います。 それぞれの区画の役割を簡単に紹介しましょう。

左上に表示されているのは、さっき作成した「R Script（アールスクリプト）」です。スクリプトとはコードを書いた文書のことで、ここ*2にコードを書いていきます。

左下には「Console（コンソール）」と書いたタブがあります。ここはRというプログラムを実行する場所です。スクリプトを実行すると、コードがこの画面に飛んできてコードを実行し、続いて出力結果が表示されます。コードに誤りがあれば、エラーメッセージが表示されます。

右上には「Environment（エンバイロンメント, 環境）」というタブがあります。ここには、読み込んだデータや定義した関数など、現在Rが扱っているもの（オブジェクト, 対象物）の概要が表示されます。

右下には下のようなタブがあります。

• Files（ファイル）：保存したスクリプトやグラフがファイルとして表示されます。
• Plots（プロット）：グラフを描くと、このタブに表示されます。
• Packages（パッケージ）：機能拡張パッケージを入れることで色々な解析を実行できるようになります（次説明します）。全て無料です。

拡張パッケージをインストールして機能を追加する

Rは拡張パッケージをインストールすることで、いろいろな機能を追加することができます。 標準よりもキレイなグラフを描けるようになる「ggplot2」というパッケージをインストールしてみましょう。

下の画面に示したように、PackagesタブのInstallボタンを押します。 出現した画面の2段目に、インストールしたいパッケージ名を入力して、Installボタンを押すとコンソール画面（左下）にインストールが実行している様子が流れてきます。

Rスクリプトを実行する

それでは試しに、下のコードをスクリプトエディタ（左上）にコピペして、実行してみましょう（これもChat GPTに書いてもらいました）。

# 必要なパッケージの読み込み
library(ggplot2)

# 乱数のシードを設定
set.seed(0)

# サンプルデータの生成
x <- runif(50) * 100  # 0から100までの乱数を50個生成
y <- x * 2 + rnorm(50, mean = 0, sd = 10)  # xに対して線形の関係とランダムなノイズを加えたデータを生成

# データフレームの作成
data <- data.frame(x, y)

# ggplot2を使った散布図の描画
ggplot(data, aes(x = x, y = y)) +
  geom_point(colour="blue") +  # 散布図の描画
  ggtitle('Sample Scatter Plot') +  # タイトル
  xlab('X') +  # X軸のラベル
  ylab('Y') +  # Y軸のラベル
  theme_minimal() +  # テーマの設定
  theme(panel.grid.major = element_line(colour = "gray"), panel.grid.minor = element_blank())  # グリッドの表示設定

スクリプトエディタにコピペした後、コード全体を選択して、右上にあるRunボタンを押します。

グラフを保存する

さっきのコードがうまく実行できていれば、右下のPlotsタブにグラフが表示されます。

このグラフを自分のパソコンに保存するためには、タブの近くにあるExportボタンから「Save as Image...」を押します。

下のような画面が出てくるので、ファイルの名前と画像サイズを指定します。

次はFilesタブを開いてみてください。さっき保存した画像（.png）の名前があると思います。このファイルにチェックを入れて、「More」→「Export...」を選びます。

出てくるウィンドウ（下）で「Download」を押せばダウンロード完了です。

おわりに

• 実際の操作は「習うより慣れろ！」です。まずはグラフを描かせる宿題で使ってみるといいかもしれません。
• Chat GPTに課金すると、ほとんど書いてくれますが、無料版のChat GPTでも結構教えてもらえます。
• 30回、読んでコメントくれてありがとう！

*1:csvとは「カンマで区切られた値（comma separated value）」のこと。

*2:スクリプトエディタと呼んだりします

高校生のためのデータ分析入門 (29)：キレイな分析用データセットを作成しよう

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書いてきました。今回と次回で、実際にデータを分析する準備をしていきましょう。

分析を始める前にデータをキレイにしよう

データ分析は、そもそもデータがなければ始まりません。 データは、組織の中で収集されるものだけでなく、外部機関（政府、自治体、国際機関など）から提供されるものもあります。無料で利用できるものもあれば、有料*1で提供されるものもあります。

データの源が何であれ、分析するためには、まずデータセットを「キレイな状態」にする必要があります。データを分析可能なキレイな状態にすることを、「前処理」と言ったりします。一見地味ですが、「データ分析は8割が前処理！」と言っても過言ではないほど重要なステップです。

キレイなデータセットとは

データセットは、

• 1つの対象者の情報が、1つの行に収められている
• 1つの項目（変数）が、1つの列に収められている
• 1つの値が、1つのセル（=マス）に収められている

が基本です。 下に示したのはダメな例ですが、どこがダメなのか考えてみましょう。

1つの列には１つの特性のみ収める

「後期の期末成績」を見てください。点数と5段階評価がまとめられていますね。 つまり、1つの列に2つの特性（= 属性（attribute）と言います）が格納されてしまっています。 一見すると数値が収められているように見えますが、"( )" が入っているため、文字列として認識されます。 このままだと平均点を計算するときに、年間総合評点が邪魔になってしまいます。

「所属クラブ」についても、複数の所属先がまとめて1つの列に格納されていますが、 所属のパターンが多くなり、このままでは「テニス部に入っている人は何人いるか」などを集計することが難しいです。 例えば、「運動部」「文化部」と複数の列に分けて情報を収めておく方が、使いやすいデータセットになるかもしれません。

1つの列に収める属性は1つにしておきましょう。後で属性と属性をくっつけてまとめる（例："1組", "1番" → "1-1"）のは簡単にできますから。

1つの行で1人のデータが完結している

次に「組」の列を見てください。同じ組の人の部分はセルが結合されていますね。 確かに、人間が見るときは余計な繰り返しがない方が見やすいですが、分析するためには「1行取り出せば1人のデータが完結している状態」になっている必要があります。

見出し行は1行に

データを収めた表（データテーブル）の一番上には、各列に収められている特性を示す「変数名」を書きます。 これを「見出し行（header）」と言います。 どこまでが見出しなのか分からなくなるので、見出し行は1行だけにする約束になっています。

入力は文字情報のみ（できれば半角英数だけ）

ExcelやGoogleスプレッドシートでは、セルに色をつけることができますよね。「血液型」は色分けされていて見やすくなっていますが、解析ソフトには色の情報は反映されません。 文字として入力した情報だけが読み取られます。また、2組1番の宍粟さんは前期の期末試験は欠席でしたが、このセルに斜線を引いておいても解析ソフトには読み込めません。欠測値には「NA（not available）」と入れておきましょう。

自分でデータセットを作る場合は、慣れるまでは「変数名を含め、半角英数字だけ*2使う」とした方が余計なトラブルが少ないです。さっきのデータの中に1箇所、誤って入力されている部分があるのが分かりますか？

1組2組の神戸さんの数学の中間結果だけが全角で入力されちゃってます。これはエラーのもと！

上記に注意して作成し直すと、次のようになります。

横型データと縦型データ

さっき「1行に1人分」と説明しましたが、これは分析の方針によります。 例えば、1回の試験を分析単位にする場合は、下の表のように1行ごとに試験の結果が入っている方が扱いやすいです。

1人の生徒につき4行分必要になるので、元のデータよりも縦長になりますね。 元のデータセットのように、反復して測定した結果（= テストの点数）を横に並べたものを横型データ、あるいは横持ちデータ（wide format data）と言います。 これに対して、反復測定した結果を縦に並べたものを縦型データ、あるいは縦持ちデータ（long format data）と言います。

横型と縦型は互いに変換することが可能で、用いる解析方法によって選択します。

複数のデータテーブルを統合して使う

これまでデータセットは最初から1つの塊として収集（あるいは提供）されるものとして話してきましたが、実際はいくつかのデータテーブルに分かれていることが少なくありません。

例えば、生徒の組と所属クラブのデータセットは、下の2つのデータテーブルを元にして作成することができますね。

「生徒番号」によって2つのデータが関連付けられています。このように、複数のデータテーブルに分けて保管された一連のデータの集合を、関係データベース（relational database）と言います。

「生徒番号」のように、データテーブルを結びつけるための列を「キー（key）」と呼びます。キーとなる項目は、重複や空欄があってはいけません（同姓同名がいる可能性があるので、名前はキーにしない方がいいです）。

場合によっては複数の項目を組み合わせてキーにすることがあります。 例えば、病院の入院記録データは、患者ごとに固有のカルテ番号だけではキーになりません。同じ人が複数回入院する可能性があるからです。しかし、同じ人が同じ日に2回入院することはないので、カルテ番号と入院年月日を組み合わせればキーにすることができます。

なぜ、わざわざ複数のデータテーブルに分けるんだろう？と思うかもしれませんが、その方が整理・管理が簡単だからです。管理するときは分けておく方が便利ですが、分析するときは1つにまとめる必要があります。

おわりに

• 自分でデータセットを準備するときは、半角英数に限定しておくと良いと言いましたが、外部から提供されるデータを扱うときはそうはいきません。全角を半角に直したり、文字列から数値だけを切り出したりするスキルが必要になります。
• データセットを扱う場合は個人情報にも気をつけましょう。名前、住所、電話番号など個人を特定できる情報は、顧客管理としては必要ですがデータ分析には不要なものが多いです。
• 次回：高校生のためのデータ分析入門 (30)：解析環境を準備しよう！ - ねこすたっと

*1:情報は価値ある商品になりえます

*2:数字から始まる変数名や、一部の記号は受け付けてくれない場合があります。また、単語と単語の間にスペースを入れると、何個入っているのか分からなくなるのでやめましょう。

高校生のためのデータ分析入門 (28)：ここまでの総復習！

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書いてきました。そろそろ終盤なので、登場した用語をまとめて確認しておきます。

変数

変数は、数や個数を表す量的変数（quantitative variable）と、 対象の性質を表す質的変数（qualitative variable）に分けられると説明しました。

necostat.hatenablog.jp

「〇〇変数」は他にもいっぱい登場しました（一部初登場あり）。

• カテゴリー変数（categorical variable）：質的変数と同じ意味（名義変数に限定して使うこともあるかも）
• 2値変数（dichotomous variable）：カテゴリー数が2つだけの変数
• 連続変数（continuous variable）：整数未満の数値も取る変数
• 離散変数（discrete variable）：整数だけしか取らない変数。質的変数 + 個数・回数を表す量的変数。
• 順序変数（ordinal variable）：質的変数のうち、カテゴリーに自然な順序がある変数
• 名義変数（nominal variable）：質的変数のうち、カテゴリーに自然な順序がない変数

数値で要約

質的変数の分布は、度数（frequency）と割合（proportion）で要約します。 割合と率（rate）との違いも説明しましたね。

量的変数の分布は、

• 中心位置：平均値（mean）、中央値（median）
• 分布の広がり：標準偏差（standard deviation）、四分位範囲（interquartile range）、範囲（range）

で要約します。

necostat.hatenablog.jp

グラフ化

質的変数に使うグラフとして、棒グラフ（bar chart）や円グラフ（pie chart）を紹介しました。

量的変数に使うグラフとしては、ヒストグラム（histogram）、箱ひげ図（box-whisker plot）、密度プロット（density plot）がありました。

2つの量的変数の関係を示すときは、散布図（scatter plot）を使えばいいんでしたね。

necostat.hatenablog.jp

necostat.hatenablog.jp

期待値・分散

期待値（expectation）とは「変数の確率重み付け平均値」、 分散（variance）とは、「各観測値と平均との差の2乗の期待値」です。分散の正の平方根が標準偏差です。

計算式がたくさん出てきて、ウンザリしたかもしれませんが、計算に便利な式変形は、知っておくとテストで役に立つかも？

necostat.hatenablog.jp

necostat.hatenablog.jp

necostat.hatenablog.jp

確率分布

連続型確率分布

正規分布（normal distribution）は、「山ひとつ・左右対称・極端な外れ値なし」が特徴で、連続変数が従う確率分布の代表です。

necostat.hatenablog.jp

検定の話で登場したカイ2乗分布（chi-square distribution）やt分布（t distribution）も連続型確率分布です。

離散型確率分布

二項分布（binomial distribution）は、「N回の試行で成功が出る回数」の分布です。 試行が1回の場合は、ベルヌーイ分布（bernoulli distribution）という名前でしたね。

necostat.hatenablog.jp

ポアソン分布（Poisson distribution）は、「稀にしか起こらないことの回数」の分布で使います。

necostat.hatenablog.jp

統計的推定

標本（sample）を調べて、母集団（population）の特性を統計学にもとづいて推測することを、統計的推定（statistical inference）といいます。推定には誤差（error）がつきもので、それには

• 系統誤差（systematic error）
• 偶然誤差（random error）

の2種類があるという話をしました。

necostat.hatenablog.jp

necostat.hatenablog.jp

推定値として、最もありそうな1点を推定することを点推定（point estimation）、ある程度の幅をもって推定することを区間推定（interval estimation）といいました。

区間推定の表し方として、95%信頼区間（95% confidence interval）がよく使われます。「何が95%なのか」は復習してください。

necostat.hatenablog.jp

統計的仮説検定

標本で大小関係を調べることで、母集団の大小関係について判断を下すことを統計学的仮説検定（statistical hypothesis testing）といいます。ここでは大事な用語がたくさんでてきました。

• 帰無仮説（null hypothesis）：主張したい仮説を否定したもの
• 対立仮説（alternative hypothesis）：主張したい仮説
• P値（P-value）：帰無仮説が正しいという仮定のもとで、標本よりも極端なデータが観察される確率
• 有意水準（significant level）：得られたP値が大きいかどうか判断するために、事前に決めておいた基準

検定をするときは有意水準の他に、大小関係の方向を限定した片側検定（one-sided test）を使うのか、どちらが大きくても構わない両側検定（two-sided test）を使うのか、も事前に決めておかなければいけません。

necostat.hatenablog.jp

P値の求め方を分類して説明しました。ちょっと難しめでしたね。

necostat.hatenablog.jp

質的変数に使う検定

カテゴリー変数では、まずカイ2乗分布（chi-square distribution）を押さえておきましょう。 使えない状況があることも覚えておきましょう。

necostat.hatenablog.jp

量的変数に使う検定

量的変数では、t検定（t test）が基本です。こちらも使用に際して注意が必要な状況があることを覚えておきましょう。

necostat.hatenablog.jp

相関と回帰

相関

相関（correlation）は、2つの変数の間にある直線的関係のことで、相関係数（correlation coefficient）を用いて示しました。 相関係数がどのように計算されるか、その元になる共分散（covariance）とともに説明しましたね。

necostat.hatenablog.jp

回帰

回帰（regression）とは、変数間の関係性を関数で表すことでした。相関と違って、「上流・下流」の区別があります（それぞれ下のように呼びます）。

• 「上流」の変数（原因）：説明変数（explanatory variable）、独立変数（independent variable）
• 「下流」の変数（結果）：応答変数（response variable）、従属変数（dependent variable）

necostat.hatenablog.jp

線形回帰モデル

応答変数が連続変数の場合には、線形回帰モデル（linear regression model）が使われます。説明変数の関数として応答変数の条件付き期待値が与えられ、そこに誤差が加わって実際の観測値が得られると考えます。

応答変数は連続変数1つだけですが、説明変数はカテゴリー変数でもOKで、複数あっても構いません。直線だけじゃなくて曲線も当てはめることもできることを紹介しましたね。

necostat.hatenablog.jp

necostat.hatenablog.jp

necostat.hatenablog.jp

necostat.hatenablog.jp

一般化線形モデル

離散型の応答変数も扱えるように線形回帰モデルを拡張したのが一般化線形モデル（generalized linear model）でしたね。 アウトカムが2値変数の場合に用いられるロジスティック回帰モデル（logistic regression model）と、アウトカムが少ない回数の場合に用いられるポアソン回帰モデル（poisson regression model）を紹介しました。

necostat.hatenablog.jp

necostat.hatenablog.jp

データ分析全般

ひとくちにデータ分析と言っても、その目的は様々です。データに溺れて進む方向が分からなくなってしまわないようにしたいです（言うは易し、ですが）。

necostat.hatenablog.jp

necostat.hatenablog.jp

データ分析はデータだけを見ているわけではありません。必ずと言っていいほど、何らかの「仮定・仮説」（=モデル）を通してデータを見ています。 そして、この仮定が適切かどうかをデータのみで判断することはできません。そこで生きてくるのが、その領域の専門家の知識と経験だと思います。

おわりに

• 統計学で大事な基礎用語・知識はまだまだあると思いますが、「高校生のための」と言う割には結構詰め込んだんじゃないかなと思ってます。お疲れ様でした！
• 高校生でも使えるデータ分析環境があるので、次回と次々回で紹介したいと思います。「え、高校生だから実際にデータ分析する機会なんてない...」と思ってるあなた！機会がないんじゃなくて、使える環境がないだけかもしれませんよ？部活とか文化祭とか、分析するネタは高校生にもあると思います。

高校生のためのデータ分析入門 (27)：量的変数を比較するとき、基本はt検定！

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (26)：カテゴリー変数を比較するとき、基本はカイ2乗検定！ - ねこすたっと

量的変数で比べたいのは代表値

例えば、隣のクラスと数学の点数を比べるとき、クラスの平均点で比べることが多いんじゃないでしょうか。 2グループ間で量的変数の平均値を比較するときに用いられる検定がt検定（t test）です。 カイ2乗検定は3つ以上のグループを一度に比較でも用いることができましたが、t検定は3つ以上のグループを一度に比較することはできません（2つを選んで比較する必要があります）。

以前、P値の計算方法についていくつかパターンを紹介しましたね。 t検定（t test）は、検定統計量と確率分布を使ってP値を求めるタイプの検定です。

T統計量

用いられる統計量（T統計量）は、 2つの標本の平均を、分散を 、標本数を とすると、次の式で計算されます*1。

2グループの平均値の差が大きくなればなるほど、T統計量は大きくなります。 また、平均の差が同じでも、分布のバラツキが小さいほどT統計量は大きくなります。 平均の差を分布の分散を基準にして定量化しているわけです。

正規分布の話をしたときに、「標準化正規分布」というものが出てきました。変数Xが正規分布に従うとき、下のように変形することでZはN(0,1)に従う、というものです。

これは「変数Xが平均μからどれくらい離れているか」を、正規分布の標準偏差σを基準にして定量化するというものでした。T統計量の考え方も同様です。

t分布

しかし、T統計量からP値を計算するときに用いる確率分布は標準正規分布ではありません。下図の赤線グラフのような形をしている、t分布（t distribution）という確率分布です。

正規分布（青）によく似ていますが、裾が正規分布よりも厚くなっています（つまり、中心から外れた値を取る確率が正規分布よりも多い）。 これは、母集団の分散が分かっている値として与えられているか（→正規分布）、標本から推定しないといけないか（→t分布）の違いです。

カイ2乗分布と同じように、t分布も自由度（degree of freedom）によって形状（裾の厚み）が変わります。自由度が大きくなり、裾が薄くなって正規分布に近づいていきます（下図）。

自由度をどう決めるかはちょっと複雑なので、ここでは説明しませんが、サンプル数が多いほど、使用するt分布の自由度も大きくなるとだけ理解しておいてください。

標本から得られたT統計量よりも極端な値になる確率、つまりP値は、t分布で下の部分の面積として求めることができます。下の例では、両側P値を求めています（P値の両側・片側の話はこちらの記事に追加しました）。

t検定を使うまでのステップ

順序変数にt検定は使えない

t検定は平均値を比較する検定方法なので、平均値に意味がないような変数の場合に用いることは適切ではありません。

例えば、「猫が好きですか？」という質問に対して、

• 0 = まあまあ好き
• 1 = 結構好き
• 2 = モフモフ〜ごろごろ〜（=めっちゃ好き）

で回答してもらったとします。回答は明らかに順序がありますが、0→1と1→2が同じ程度を意味しているとは限りません。1単位の変化の意味が異なるので、平均を取っても意味がありません。このように「順序はあるが、割り振られた数値の差に意味がない変数」を、順序変数（ordinal variable）と呼びます。 順序変数を比較するときは、マンホイットニーU検定（Mann-Whitney U test）****2という検定方法が使われることが多いです。

変数の分布か正規分布かどうか

t検定において、T統計量がt分布に従うためには、変数Xが正規分布することが必要とされます。そのため、t検定を使う前に、まず変数Xが（それぞれのグループで）正規分布しているかどうかを検定するように推奨している本が多いと思います。

しかし、正規性を確認する検定は必要ないと説明しています。理由は、

• t検定は正規分布から多少ズレていても問題なく使える
• サンプル数が多かったら、標本平均の分布*3は正規分布とみなせるようになる

などです。なので、ヒストグラムなどで概ね山が1つに見えていればOKです。

もし、ヒストグラムで正規分布に見えない分布で、サンプル数もそんなに多くないときは、先程紹介したマンホイットニーU検定を用います。この検定は、変数について全体の中での順序だけしか考慮しないので、正規分布かどうかを気にする必要がなくなります。

2つの標本の分散が等しいかどうか

最初の方で「差をバラツキで定量化する」という話をしました。比べたい2つのサンプルの分散が同じ場合・違う場合で、T統計量の分母の計算が少し変わります。

分散が同じ値として計算するt検定をスチューデントのt検定（Student's t test）、分散か異なっているとして計算するt検定をウェルチのt検定（Welch's t test）と言います。

まず2つの標本分散が同じかどうかを検定で確かめてから、どちらのt検定を使うか選ぶことを推奨している本も多いですが、常にウェルチのt検定を使って問題ありません。

おわりに

• t検定は「正規性や等分散性を確認して選ぶ」というお作法にとらわれすぎない方がいいです。
• 3つ以上のグループで量的変数を比較するときは、分散分析（analysis of variance）という手法を使います。分散分析とマンホイットニーU検定は名前だけでも覚えておくといいでしょう。
• 次回：高校生のためのデータ分析入門 (28)：ここまでの総復習！ - ねこすたっと

*1:Welchのt検定の場合

*2:別名：ウィルコクソン順位和検定, Wilcoxon rank sum test

*3:標本を抽出して平均を取ることを繰り返したときの標本平均の分布

高校生のためのデータ分析入門 (26)：カテゴリー変数を比較するとき、基本はカイ2乗検定！

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (25)：P値はどうやって計算するの？ - ねこすたっと

ほとんどはカイ2乗検定でOK！

前回、サイコロが公平かどうかを確かめる方法として、カイ2乗検定を紹介しました。 まずはカイ2乗分布とはどんな確率分布なのか見てみましょう。

そもそもカイ2乗分布って？

カイ2乗分布（chi-square distribution）は、標準正規分布に従う独立な変数を2乗して足してできた変数が従う確率分布です。つまり、 のとき、 はカイ2乗分布に従う、ということです。

カイ2乗分布について、押さえておくべき特徴は次の2つ！

• 変数が正の範囲にしか分布しない（2乗して足したものは必ず正だから）
• 足し合わせる個数によって形が変わる（足す個数kが大きい方が広くバラつきそう）

確率密度関数はちょっと複雑なので紹介しませんが、足す個数kの値によってどのように分布の様子が変わるのか、下の図をみてください（wikipedia - カイ2乗分布）。

このkは、カイ2乗分布の形状を決めるパラメータで、自由度（degree of freedom, df）と呼ばれます。自由度kのカイ2乗分布を と書くので、数式を使うと、

と書くことができます。

カイ2乗検定で期待値からのズレを評価する

カイ2乗検定（chi-square test）は、理論値・期待値（E）と実際の観測値（O）から、カイ2乗統計量を計算し、これがカイ2乗分布に従うことを使ってP値を求めることを前回説明しました。例えば、カテゴリー数がm個の場合は、下の関係が成り立ちます。

ここで、自由度がmではなくm-1になっている理由は、「m-1のカテゴリーに入る度数が決まったら、残り1つのカテゴリーに入る度数は自動的に決まるから」です。自由度の説明がもう少し読みたい人は、下の記事を参考にしてください。

best-biostatistics.com

これを使って、カテゴリー変数をどのように比較できるのか見ていきましょう。 例えば、文系クラスと理系クラスで猫好き・犬好きを調査したら、下の表になったとしましょう。

「文系と理系で猫派・犬派の割合が変わるか」ということを検証したいときは、まずこれを否定した帰無仮説を考えるんでしたね。帰無仮説は「文系と理系で猫派・犬派の割合は変わらない」です。では、帰無仮説が正しいとき、さっきの表がどうなっているはずでしょうか？

文系・理系で猫派の割合が変わらないと仮定すると、それぞれの猫派の割合は学年全体における猫派割合 と同じになるはずです。文系は100名いるので、猫派の人数は、100×190/250 = 76名いるはずです。この76名が、帰無仮説のもとでの期待値ということになります。

「文系・猫派」の期待値は、（文系の周辺度数*1=100）×（猫派の周辺度数=190）/（全体数=250）で求められました。 「文系・犬派」、「理系・猫派」、「理系・犬派」も同じように求めることができますが、実際には「文系・猫派」が求まれば、他のマス目に入るべき人数は自動的に決まります（例：「文系・犬派」= （文系の周辺度数=100）- （「文系・猫派」の期待値=76）= 24）。

期待値を表にまとめると、

となります。観測値と期待値が分かればカイ2乗値は計算できますね。

X²は自由度1のカイ2乗分布に従うので、これを使って と計算できます（つまり、割合は有意に異なっている）。 なぜマス目は4つあるのに自由度は1なのかというと、先程説明したように1つのマス目が決まれば残りは自動的に決まるからです。

ちなみに、「文系・理系で猫派・犬派の割合が異なっているか」ということと、「猫派・犬派で文理の割合が異なっているか」ということは全く同じことです（実際にX²を計算しても同じになります）。なので、どちらの項目から捉えるかを区別せずに「2つの項目の間に関連性があるか」と読み換えると良いです。

カテゴリー数が多い場合は？

例えば、「文系・理系」ではなく「1組〜5組」、あるいは「猫派・犬派」ではなく「猫派・犬派・爬虫類派」のように、カテゴリー数が3つ以上になってもカイ2乗検定は使えます。 それぞれの項目から2つのカテゴリーを選んできて比較するという意味ではなくて、クラスによって「猫派・犬派・爬虫類派」の分布が変わるか、もう少し言えば「2つの項目（クラス・何派か）の間には関連性があるのか」を検定できる、という意味です。

関連性を確かめたい2つの変数のカテゴリー数がm, nであった場合、m×n個のマス目がある表ができます。さっきと同じように、期待値を求めて、観測値との違いをX²値として計算してやればいいです。 ただし、カイ2乗分布は、自由度(m-1)×(n-1)のものを使います。

例えば、1つ目の項目が「1組〜5組」の5カテゴリー、2つ目の項目が「猫派・犬派・爬虫類派」の3カテゴリーなら15マスありますよね。この15マスについて、観測値と期待値の差をもとにX²値を計算して、自由度が(5-1)×(3-1)=8のカイ2乗分布に従うことを利用してP値を計算します。

m=n=2とすると、2×2表のときに自由度1のカイ2乗分布を用いたことと整合性があることが確認できますね。

カイ2乗検定が使えないとき

期待されるマス目の度数が小さい場合

期待される度数が小さいときは、カイ2乗検定が不正確になるので使用を避けるべきと言われています。期待度数が少ない基準としては、下のものが一般的です。

• 期待度数が 5 以下のマスが全体の 20% 以上ある場合
• 期待度数が 1 以下のマスが 1 つでもある場合

この条件に引っかかってしまう場合は、カイ2乗検定ではなくフィッシャー正確検定（Fisher exact test）を使うように勧められることが一般的です。これには色々と問題もありそうですが、検定の名前くらいは覚えておきましょう。

同じ人に2回調査をしている場合

例えば、学校で「世界ネコ歩き（岩合光昭さん・NHK）」の鑑賞会があったとします。見る前と見た後に、40人のクラスメートに猫派・犬派を聞いたとします。

見る前から猫派だった人は、当然見た後も猫派ですよね。それを無視して、「見る前後で関連がない」として期待値を求めることには意味がありません。文系・理系で比べたときは1人につき1回しか調査しなかったのでこのような問題は起こりませんでしたが、「今回は同じ人に2回調査をしている」という点がポイントです。同一対象者の前後を比較する場合は、データの中に対応関係（ペアとなる関係）が含まれることになります。このようなデータを「対応のあるデータ（paired data）」と呼びます。 対応のあるデータの例としては、前後比較の他に、双子をペアにして調査するケースがあります。

対応のあるデータで割合を比べるときには、マクネマー検定（McNemar test）を用います。詳細は割愛しますが、名前だけでも覚えておくといいでしょう。

おわりに

• 理論値に適合しているかどうかをみるカイ2乗検定を「適合度検定（test of goodness of fit）」、2つの要因に関連があるかどうかをみるカイ2乗検定を「独立性検定（test of independence）」と呼びます。
• 次回：高校生のためのデータ分析入門 (27)：量的変数を比較するとき、基本はt検定！ - ねこすたっと

*1:そのカテゴリーに関しての合計数のこと。