ブートストラップ（bootstrap）法で信頼区間を求める（bootパッケージ）[R]

例示のための元データの作成
bootパッケージを使って信頼区間を計算する
- boot( )を使ってブートストラップサンプル毎の統計量を計算する
- boot.ci( )を使ってブートストラップ信頼区間を計算する
信頼区間を計算するアルゴリズム色々
おわりに
参考資料

サンプルを用いて母集団の特性を推定する際は誤差がつきもの。そのため点推定値だけではなく信頼区間をつけるのが当たり前になっているわけだが、正規分布など特定の分布を仮定することが怪しいときがある。

ブートストラップ法は、元サンプル（original sample）から重複を許した復元抽出を繰り返して作成した標本（ブートストラップサンプル, bootstrap sample）を使って推定誤差を分析する方法。元サンプルの平均・標準偏差を有する正規分布（など）から乱数を発生させる「パラメトリック・ブートストラップ法」という方法もあるが、ブートストラップと言えば大抵は次の「ノンパラメトリック・ブートストラップ法」のこと。

元サンプルを母集団に見立てて
元サンプルと同じサンプル数Nを*1
重複を許して*2抽出することを
何回も繰り返す（1000-2000回）

B個のブートストラップサンプルを作れば、興味ある統計量（平均値とか中央値とか）もB個できて、その中にはたまたま大きい値・小さい値になったものがあるわけです。計算される統計量の幅を使って推定の幅を求めてやろうという方法なので、あまり詳しい理論とか計算を知らなくても（PCが頑張ってくれれば）信頼区間が計算できるという便利な方法です。

例示のための元データの作成

ここではブートストラップ法の提唱者であるEfron先生・Tibshirani先生の教科書に載っているデータを例に使う。 15人のLSATとGPA（成績のスコア）の相関係数を信頼区間付きで推定してみる。

元データは次のコードで作成。

lsat <- c(576,635,558,578,666,
          580,555,661,651,605,
          653,575,545,572,594)
gpa <- c(3.39,3.30,2.81,3.03,3.44,
         3.07,3.00,3.43,3.36,3.13,
         3.12,2.74,2.76,2.88,2.96)
data <- data.frame(lsat,gpa)

相関係数rの標準誤差が

$SE(r) = \sqrt{\frac{1-r^2}{n-1}}$

95%信頼区間が

$CI(r) = r \pm t_{df=n-2} SE(r)$

となることを使って手計算すると、相関係数rは0.776（95%CI: 0.399, 1.154）と計算される。

bootパッケージを使って信頼区間を計算する

大まかな流れは以下のとおり。

boot( )を使ってブートストラップサンプルを作成し、それぞれのブートストラップサンプルで統計量を計算する
boot.ci( )を使ってブートストラップ信頼区間を計算する

boot( )を使ってブートストラップサンプル毎の統計量を計算する

元サンプルから母集団の分布のパラメータを推定して、想定した特定の確率分布から乱数を発生させる「パラメトリック・ブートストラップ法」を実装することもできる（sim="parametric"）が、使う機会がほとんどなさそう（ちなみに`sim="ordinary"だと、「n個の観測値があるサンプルから、重複を許してn個サンプリングする」という「いつもの」方法を指定）。

知っておいた方がいい引数は3つ。

data：元サンプル（ベクトル、行列、データフレーム）
statistic：データに対して計算したい統計量。関数を定義して与える。この関数では第1引数はデータ、第2引数はブートストラップサンプルを定義する方法（index, frequency, weightのいずれか）。stypeという引数で使用するサンプリング方法を指定できるが、デオフォルトのindexを使う方法を知っていれば大体事足りそう。
R：サンプリング回数。1000-2000回は必要だが、元サンプルが少なかったらいくら増やしても頭打ちになる。

統計量を計算する関数を書くところが少しハードルが高そう。例えば、LSATとGPAの相関係数を求める関数は次のとおり。シンプルに2つしか引数を使わないようにして"get_cor"と名前をつけた。

get_cor <- function(d,i){
  x <- data[i,"lsat"]
  y <- data[i,"gpa"]
  r <- cor(x,y)
  return(r)
}

下のコードのように、boot( )に必要な3つの引数を指定する。

set.seed(1234)
boot_out <- boot(data,
                 statistic = get_cor,
                 R = 2000)

boot.ci( )を使ってブートストラップ信頼区間を計算する

前述のboot( )で作ったオブジェクト（boot_out）からboot.ci( )を使って信頼区間を計算する。信頼区間を計算するアルゴリズムは以下の5種類が用意されている。

"norm"：正規分布への近似を使った方法（the first order normal approximation）
"basic"：ベーシック法（the basic bootstrap interval）
"stud"：スチューデント化t法（the studentized bootstrap interval）
"perc"：パーセンタイル法（the bootstrap percentile interval）
"bca"：BCa（=Bias Corrected and acceralated）法

それぞれの方法の大まかな説明は後述するが、分からなかったらBCa法を選んでおけばよい。コードは次のとおり。

boot_out <- boot(data,
                 statistic = get_cor,
                 R=2000)

どの方法を使うかは引数typeで指定。type="all"としておけばスチューデント化t法を除いた全ての方法の結果が表示される（スチューデント化t法では統計量だけではなく、統計量の分散もブートストラップ法で推定しないといけないから）。

boot.ci(boot_out, type = "all")

> boot.ci(boot_out,type = "all")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL : 
boot.ci(boot.out = boot_out, type = "all")

Intervals : 
Level      Normal              Basic         
95%   ( 0.5187,  1.0371 )   ( 0.5905,  1.0955 )  

Level     Percentile            BCa          
95%   ( 0.4573,  0.9622 )   ( 0.3138,  0.9397 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
Warning message:
In boot.ci(boot_out, type = "all") :
  bootstrap variances needed for studentized intervals

ちなみに、元サンプルにおける統計量は$t0、ブートストラップサンプルにおける統計量は$tで取り出せる。

> boot_out$t0
[1] 0.7763745

> mean(boot_out$t)
[1] 0.7748804

> sd(boot_out$t)
[1] 0.1322489

以下のコードでヒストグラムを描いてみる。

library(tidyverse)
boot_out$t %>% as.data.frame() %>%
  rename(statistics=V1) %>%
  ggplot(aes(x=statistics)) +
  geom_histogram(fill="navy", alpha=0.25) +
  geom_vline(xintercept=boot_out$t0, colour="navy")+
  theme_bw()

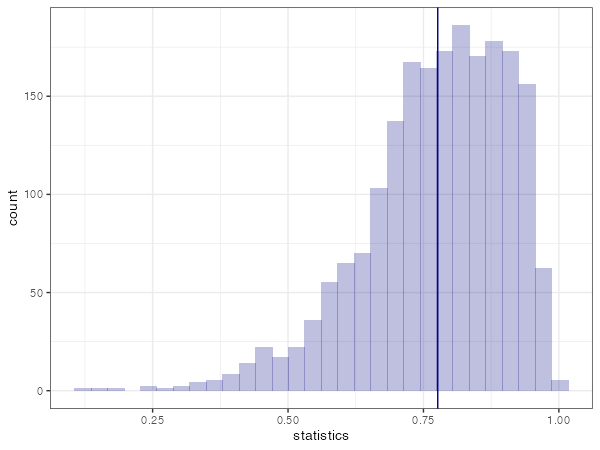
図1：ブートストラップサンプルにおける相関係数の分布（ヒストグラム）と元サンプルの相関係数（垂直線）

信頼区間を計算するアルゴリズム色々

「ひと口にブートストラップ信頼区間といっても5種類あること」と「よく分からなかったらBCa法でよいこと」さえ押さえていれば十分な気もしますが、何となく分かったつもりで各アルゴリズムを説明してみる（詳細は末尾の資料を参照のこと）。

表記のルール

なるべく数式は使わないつもりだが、似たような用語が多くて使い分けも混乱するので表記ルールを決めておく。

$N$ ：元サンプルのサンプルサイズ
$B$ ：抽出するブートストラップサンプルの個数
$\theta$ ：興味ある統計量（前述の例では相関係数）の真（=母集団）の値
$\hat{\theta}_0$ ：元サンプルにおける統計量の値
$\hat{\theta}^*_i$ ： $i$ 番目のブートストラップサンプルにおける統計量の値（ブートストラップサンプルについて一般的に述べるときは $i$ を省略するときがある）。
$E [ \hat{\theta}^*$ ]：B個のブートストラップ統計量の平均
$var [ \hat{\theta}^*$ ]：B個のブートストラップ統計量の分散

最後の2つは、

$\begin{align} E \left[ \hat{\theta}^* \right] &= \frac{1}{B}\sum_{i=1}^B \hat{\theta}^*_i \\ var \left[ \hat{\theta}^* \right] &= \frac{1}{B-1} \sum_{i=1}^B \left( \hat{\theta}^*_i - E \left[ \hat{\theta}^* \right] \right)^2 \end{align}$

と計算される。

バイアス

ブートストラップサンプルから計算したB個の統計量の平均値と、元サンプルから計算された統計量の差をバイアスと呼ぶ。

$\begin{align} bias &= E \left[ \hat{\theta}^*_i \right] - \hat{\theta}_0 \end{align}$

つまり、前の例でのバイアスは、

> mean(boot_out$t) - boot_out$t0
[1] -0.001494062

と計算される。

統計量の推定誤差

統計量の推定誤差は標準誤差（standard error, SE）で表される。これは「ブートストラップ毎に統計量の推定がどれくらいバラついているか」ということなので、ブートストラップ分散推定量 $var [ \hat{\theta}^*$ ] を使う。この分散の平方根をとると標準誤差になる（手計算で確認）。

> sd(boot_out$t)
[1] 0.1322489

正規分布への近似法

95%信頼区間といえば「平均±1.96SE」だが、この平均とSEにブートストラップサンプルから推定したものを使おうという方法。「正規分布に近似が難しそうだからブートストラップしようと思ったのに、なぜまた正規分布なの？」あるいは「そもそもこれはブートストラップ信頼区間といっていいのか」という声もある（かも）。

前述の例では信頼区間上限値が相関係数の取りうる範囲を超えており、ブートストラップしたのに問題が解決されていない。

ベーシック法

ベーシック法での信頼区間は、以下のように定義される。

$CI_\alpha = \left( 2\hat{\theta}_0 - q_{1-\alpha/2}, 2\hat{\theta}_0 - q_{\alpha/2} \right)$

ここで、[tex: q{\alpha/2}] と [tex: q{1-\alpha/2}] はそれぞれブートストラップサンプルの分布から得られる統計量の分位点（95%信頼区間なら2.5パーセンタイル値と97.5パーセンタイル値）。

こちらも正規分布への近似と同様、信頼区間上限値が相関係数の取りうる範囲を超えてしまっている。

スチューデント化t法

スチューデント化とは「推定値のとの差を推定誤差で割る」ということ。正規分布の標準化とおんなじようなものだが、このときは母集団の分散は既知である。これに対して、サンプルから平均だけでなく分散も推定して、推定した分散から得た値を分母に使おうというのがt分布。

スチューデント化t法では、下の式で計算されるブートストラップt推定量の分布を使って信頼区間の限界値を求める。

$t^* = \frac{\hat{\theta}^* - \hat{\theta}_0}{\hat{SE_{\hat{\theta}}}}$

この方法では前述のように、統計量のブートストラップ推定値（「代表」推定値とか言った方が誤解がないかもね）だけではなく、その推定誤差が必要になる。推定誤差がブートストラップ分散推定量から導出できるときはそれを使えばいいが、その計算が簡単にできないときはさらにブートストラップを使うことになる（nested bootstrap algprism）。こうなると計算負荷がはるかに大きくなることは想像に難くない。

標準誤差の推定のことも考えないとboot.ci()で計算されないので実装が一番大変そうだが、計算負荷が高い割に幅が広くなりがちだったり、取りうる範囲外の限界値が返ってきうるので、使う機会はあまりないかも。