分割時系列解析（Interrupted Time Series Analysis）による公衆衛生介入の評価 [R]

ITSAとは
- ITSデザインに適した状況は？
インパクトモデルを選ぶ
分析実行例
自己相関を確認する
おわりに
参考文献

ITSAとは

例えば新しい政策が実施されるときなど、ある介入が集団に対して一斉に行われる場合には、介入を受けない対照群を設定することができません。

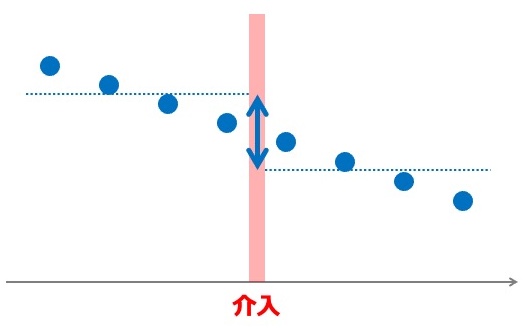
単純に介入の前後を比較するだけでは不十分です。下図では介入に無関係な減少トレンドが見られますが、介入前後で平均を単純に比べてしまうと、あたかも介入に効果があったように見えてしまいます。

正しく評価するためには、背景にあるトレンドや周期性を考慮した解析が必要で、これが分割時系列解析（Interrupted Time Series Analysis, ITSA）です。

ITSデザインに適した状況は？

分析したい状況を、

介入
アウトカム
データ

の観点で考えます。

介入の導入時期は明確である必要があります。介入前と介入後を明確に区別できなければ、適切な分析ができません。

また、アウトカムは介入に速やかに反応するものが望ましいです。介入から反応までに遅延（lag）があっても問題ありませんが、効果発現の機序を踏まえ、lagが明確に設定できることが重要です。

最後に、介入前後でアウトカムが連続的に測定されていて、利用可能であることが必須です。ルーチンで測定されているデータが適していますが、介入によってデータの測定や収集が影響されているとバイアスを生じてしまいます。

PenfoldとZhangによれば、介入前後のそれぞれにおいて最低でも8時点ずつのデータが必要とのことですが、周期性やデータの変動、効果の大きさなどの影響を受けるので単純ではなさそうです。

少なくとも、

トレンドが一定と考えられる範囲で時点数は多い方がいい
介入前後で時点数が均等に近い方がいい

ということについては、デザインを考える段階で検討できそうです。

インパクトモデルを選ぶ

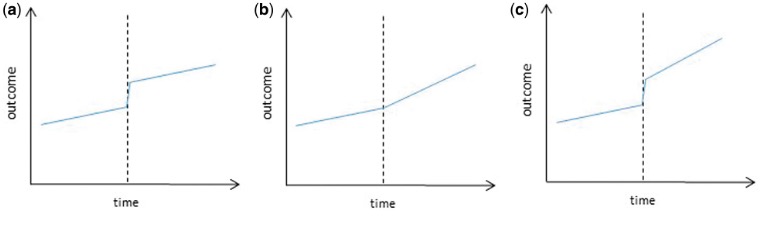
他の回帰分析と同様に、介入がアウトカムにもたらす影響について仮説（インパクトモデル）を設定することが必要です。これには主に次の3つのパターンがあります（図は Bernal JL et al. (2017) から）。

(a) 切片の変化（level change） ：
介入が実施された直後に、アウトカムの水準（切片）に顕著な変動が生じるモデル。介入が即時に影響を与え、その影響が継続することを想定している。
(b) 傾きの変化（slope change）：
介入がアウトカムの増加または減少のペース（傾き）に変化をもたらすモデル。介入の効果が徐々に現れ、時間とともに増強・減弱することを想定している。
(c) 切片と傾きの両方の変化

介入効果が出現するタイミングや持続性に関わる「遅延（lag）」を設定することもできます。

(d) 介入から遅れてslope changeが出現
(e) level changeが一過性
(f) slope changeが一過性

インパクトモデルは、既存の知見や想定している機序などを元にして事前に決めますが、lagの長さなどが異なった複数のモデルを使って感度分析を行うこともあります。

分析実行例

使用するデータ

ITSAには最低限、以下の3つの変数が必要です。

T：研究開始からの時間（月次、年次など）。サンプルデータのtimeがこれ。
X：介入前（=0）か介入後（=1）かを示すダミー変数
Y：時間 $i$ におけるアウトカム

サンプルデータ（Bernal et al. (2017)）を使って、実際に分析の流れを見ていきましょう。これはイタリアで2005年に施行された屋内での喫煙禁止法の効果を、2002-2006年の急性冠動脈イベント（ACE）による入院数を使って検証したデータです。

library(tidyverse)
data <- read_csv("sicily.csv")

> head(data)
# A tibble: 6 × 7
   year month  aces  time smokban     pop  stdpop
  <dbl> <dbl> <dbl> <dbl>   <dbl>   <dbl>   <dbl>
1  2002     1   728     1       0 364277. 379875.
2  2002     2   659     2       0 364277. 376496.
3  2002     3   791     3       0 364277. 377041.
4  2002     4   734     4       0 364277. 377116.
5  2002     5   757     5       0 364277. 377383.
6  2002     6   726     6       0 364277. 374113.

含まれている変数は以下のとおり：

year：カレンダー時間（年）
month：カレンダー時間（月）
aces：ACEによる入院数（←Y）
time：研究開始からの経過時間（←T）
smokeban：禁煙法施行前（=0）か後（=1）を示すダミー変数（←X）
pop：人口
stdpop：年齢標準化人口

ここではアウトカムとしてACE入院数をそのまま用いますが、これ以外にも標準化発生率（aces/stdpop）を使う、あるいはstdpopをオフセット項にする、などの方法もあると思います。

散布図を描く

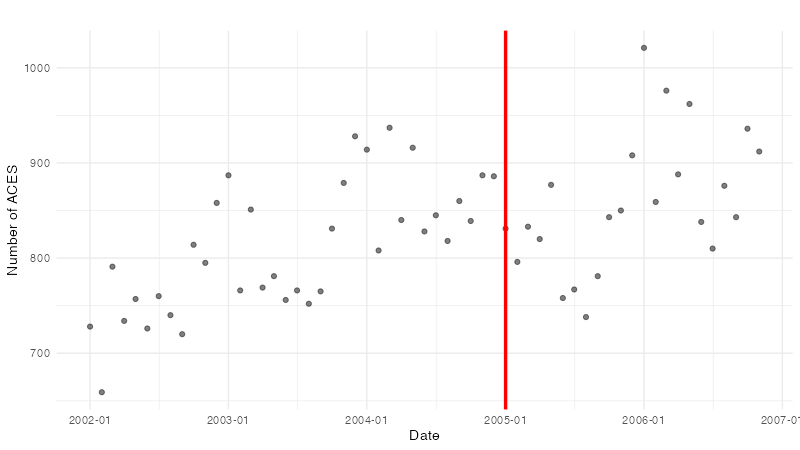
まずは散布図を作成して、背景にあるトレンドや周期性、極端な外れ値がないかを見ましょう。

なんとなく周期性はあるように見えますが、このグラフだけで判断するのは難しそうですね...。他に考慮すべき共変量がある場合は、その変数の時間依存性などを可視化して確認しておく方がいいかもしれません。

Level Change Model

介入の前後で異なった回帰直線を当てはめるだけであれば、それほど難しくないと思います。ただ、別々のデータセットで別々に推定された回帰係数を比較して、「切片や傾きの変化が統計的に有意か」などを見るのは難しいので工夫が必要です。

まず、切片の変化を想定したい場合は、以下の回帰モデルを使います。

$\begin{aligned} Y_i &= \beta_0 + \beta_1 T + \beta_2 X_i \\ \end{aligned}$

この式では、時間Tに対する傾きはXによらず一定（ $\beta_1$ ）で、X=1になると全体がY軸方向に $\beta_2$ だけ平行移動するので、目的のlevel changeは $\beta_2$ として推定されます。

Slope Change Model

次に、傾きの変化のみ想定したい場合は、以下の回帰モデルを追加います。

$\begin{aligned} Y_i &= \beta_0 + \beta_1 T + \beta_3 T_a \\ \end{aligned}$

ここで、Taは介入後からの時間を表す変数で、

介入前（X=0）のときTa=0
はじめてX=1となったときにTa=1となり、以後Tと同じように増えていく

という規則で作成します。

上記のTaに当たる変数time_afterを、下のコードで作成しておきます。

before_ban <- filter(data, smokban == 0) %>%
  slice(n()) %>%
  pull(time)
data <- data %>%
  mutate(time_after = (time - before_ban)*smokban)

介入が2005年1月（time=37）からなので、作成された変数は次のようになっています。

> data %>% slice(34:40)
# A tibble: 7 × 8
   year month  aces  time smokban     pop  stdpop time_after
  <dbl> <dbl> <dbl> <dbl>   <dbl>   <dbl>   <dbl>      <dbl>
1  2004    10   839    34       0 364700. 384052.          0
2  2004    11   887    35       0 364700. 384450.          0
3  2004    12   886    36       0 364700. 383428.          0
4  2005     1   831    37       1 364421. 388153.          1
5  2005     2   796    38       1 364421. 388373.          2
6  2005     3   833    39       1 364421. 386470.          3
7  2005     4   820    40       1 364421. 386033.          4

Level + Slope Change Model

切片と傾きの両方の変化を想定したい場合は、前述の項を両方含めます。

$\begin{aligned} Y_i &= \beta_0 + \beta_1 T + \beta_2 X_i + \beta_3 T_{a} \\ \end{aligned}$

推定してみます。

fit <- lm(aces ~ time + smokban + time_after, data=data)

> summary(fit)

Call:
lm(formula = aces ~ time + smokban + time_after, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-98.957 -38.575  -4.926  35.513 158.337 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 728.4730    18.9129  38.517  < 2e-16 ***
time          4.4534     0.8914   4.996 6.28e-06 ***
smokban     -92.9697    30.0426  -3.095   0.0031 ** 
time_after    0.6879     1.9609   0.351   0.7271    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 55.56 on 55 degrees of freedom
Multiple R-squared:  0.4418, Adjusted R-squared:  0.4113 
F-statistic: 14.51 on 3 and 55 DF,  p-value: 4.441e-07

係数の解釈は次のとおり：

(Intercept)：観察開始時のACE入院件数の期待値（解釈不要）。
time：介入前のトレンド。平均して毎年4.5件ずつ増加傾向であった。
smokban：介入による切片の変化（level change）。法律の施行によりACE入院が約93件減り、統計的に有意な変化があった。
time_after：介入前後で傾きの変化（slop change）。法律の施行後、ACE入院の増加傾向が4.5から5.1に増えたが、統計的に有意な変化ではない。

自己相関を確認する

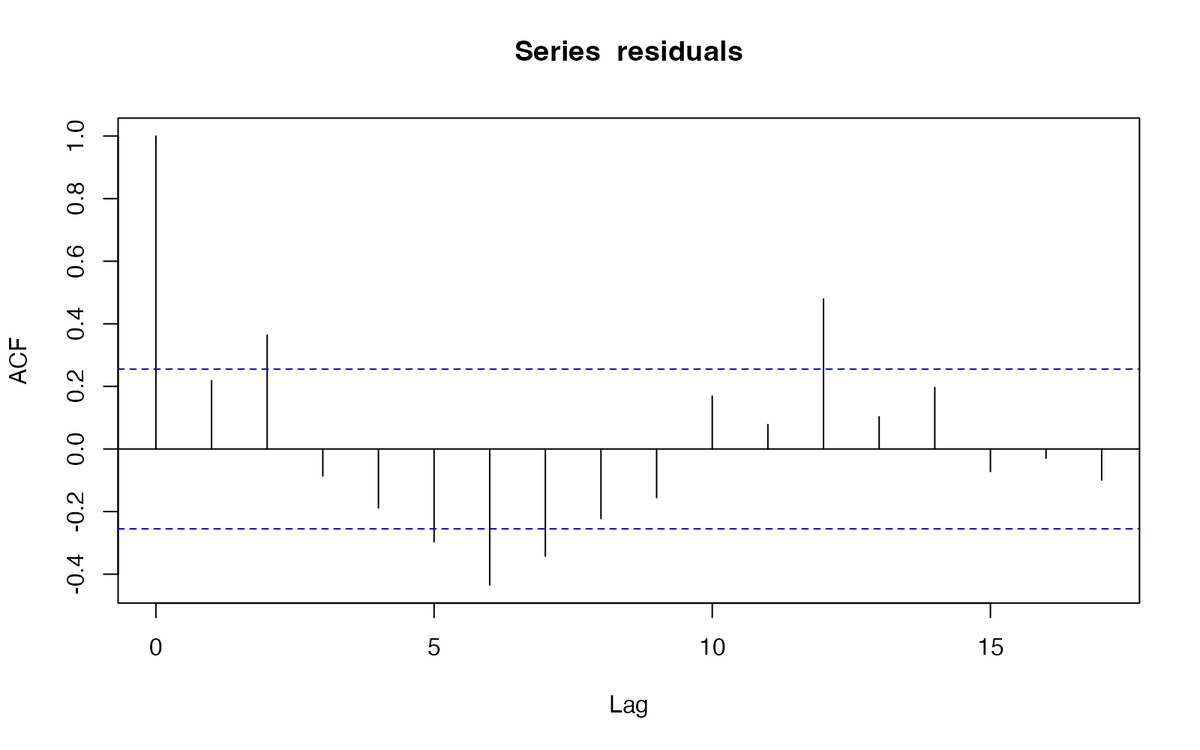
残差について、自己相関関数（autocorrelation function, ACF）を確認します。自己相関は、時点tのデータと時点t-kのデータの相関係数をラグ k の関数として示したもの。

residuals <- fit$residuals
acf(residuals, plot=TRUE)

Lag=6のときに負の相関、Lag=12で正の相関が強そうで、ACE入院件数には季節性がありそうですね。ちなみにLag=0のときは、自分自身との相関係数なので常にACF=1です。

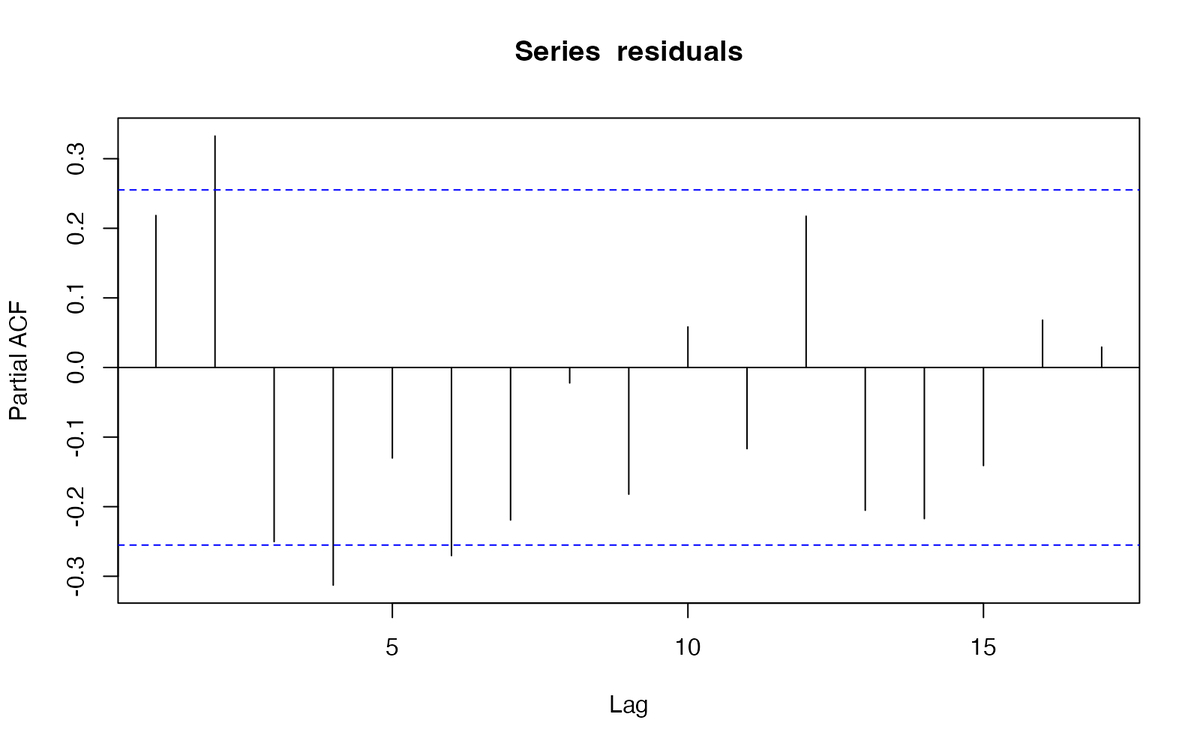
次に、偏自己相関関数（partial autocorrelation function, PACF）を確認します。偏自己相関は、時点tと時点t-kの間にあるデータ（時点t-k+1 〜 t-1）を使って、時点t, t-kのデータを回帰した残差の相関です。2つの時点間のデータの影響を取り除いて、2時点の直接的な相関を見るもの。