データの構造を要約・説明する手法
因子分析を1回しかやったことがない身ですが、備忘録として書いています。
データが持つ情報を要約したり、説明したりする手法としては、
- 主成分分析(principal component analysis, PCA)
- 因子分析(factor analysis, FA)
がある。主成分分析の目的は「変数を統合して情報を縮約すること」であり、因子分析の目的は「変数の中に共通因子(潜在因子)を見つけてデータを分解すること」である。
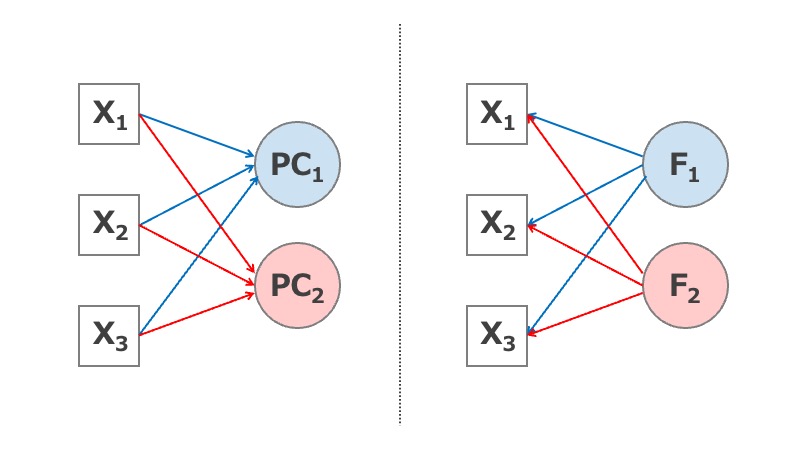
因子分析は、
- 探索的因子分析(exploratory FA, EFA)
- 検証的因子分析(confirmatory FA, CFA)
に分けられる。EFAは、潜在因子と変数の間の関係性に先行する仮説や制約を置かず、データの構成概念を探索するもの。CFAは先行する理論に基づいた因子・変数間関係が存在するかを検証するもの。EFAが「データ主導型分析」であるのに対して、CFAは「仮説主導型分析」と言える。
探索的因子分析の手順
psychパッケージを使ったEFAの手順を、以下のステップに分けてみていく。
- データの評価
- 因子数の決定
- 因子の抽出
- 因子軸の回転
- 結果の解釈
使用するパッケージとデータセット
ここではpsychパッケージのbfiデータを使う。28列のうち最後の3列は、性別、学歴、年齢なので、ここではそれらを除外した25列を使用する。データの中身が気になる人は、help(bfi)を見るか、津田裕之先生の資料*1を参照のこと。
因子軸の回転に使うGPArotationパッケージもついでに入れておこう。
library(psych) library(GPArotation) data(bfi) data <- bfi[1:25]
1. データの評価
まずデータがEFAに値するかどうかを評価する。
- 変数の型:連続変数、または5カテゴリー以上の順序変数
- サンプルサイズの目安:変数×10
- KMO(Kaiser-Meyer-Olkin)統計量:>0.6が必要
- 変数同士の相関係数:相関が強すぎる(>0.9)と多重共線性が疑われる
KMO統計量
KMO統計量は0〜1の範囲の値を取り、「偏相関係数(他の変数を調整した相関係数)の2乗和が0に近いほど、少なくとも1つの潜在変数が存在する可能性が高くなる」ことを意味しているとのこと。
psychパッケージのKMO( )を使う。
> KMO(data) Kaiser-Meyer-Olkin factor adequacy Call: KMO(r = data) Overall MSA = 0.85 MSA for each item = A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 0.74 0.84 0.87 0.87 0.90 0.83 0.79 0.85 0.82 0.86 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 0.83 0.88 0.89 0.87 0.89 0.78 0.78 0.86 0.88 0.86 O1 O2 O3 O4 O5 0.85 0.78 0.84 0.76 0.76
全体指標(Overall MSA)の値が小さいとき(<0.6)は、個別指標(MSA for each item)の値が小さい変数を除外してみる。
相関係数
変数間の相関係数はcor( )で計算できる。結果は割愛。
cor(data, use="na.or.complete")
引数useのデフォルトは"everything"になっているので、組み合わせの中で欠測が1つでもあるとエラーになる。
「ペアワイズ削除」と言えば、対比較ごとに欠測を除外する方法。例えば、変数xと変数yの相関係数を計算するときに変数zが欠測であったとしても、その症例は除外しない。
「リストワイズ削除」と言えば、解析対象の変数のうち1つでも欠測があれば、その症例は除外する方法。引数で"complete"と指定すればこれに該当。
2. 因子数の決定
EFAでは構造を探索する前に、潜在因子の数を決めなければならない。色々な決め方があって、絶対的な正解はなく、複数の基準を考慮して総合的に決めることになるのだが、今の時代は以下の方法が推奨とのこと。
- MAP基準:Minimum Average Partial (correlation) = 最小平均偏相関。清水先生の説明によると「最も効率的に相関行列を説明できる因子数を提案」してくれるとのこと。提案される因子数は少なめ。
- 情報量規準を用いる方法:BICが推奨みたい。提案される因子数多め。
- 平行分析:スクリープロットを使って選ぶ。
VSS()を使ってMAP, BICに基づいた因子数を選択する
VSS()にデータセットもしくは相関行列を渡せばMAP, BICに基づいた因子数を提案してくれる。ちなみにVSSはVery Simple Structureの略。
n:検討する因子数の上限。必要そうな因子数より少し多めを設定しておく。use:前述の相関行列を参照。ヘルプに寄ると"pairwise"か"complete.obs"を選択(多分cor()の引数useで選べるもの)。
VSS(data, n=10, use="complete.obs")
結果の中で、因子数を提案してくれているところだけ取り出すと以下のとおり。
The Velicer MAP achieves a minimum of 0.01 with 5 factors BIC achieves a minimum of -500.45 with 8 factors Sample Size adjusted BIC achieves a minimum of -166.11 with 10 factors
MAP基準によれば5因子、BICを用いれば8因子が提案された。少なくとも5因子、多くても8因子の範囲で選べとのこと。
fa.parallel( )を使って平行分析で因子数を選択する
平行分析の前に、スクリープロットの説明を。
スクリープロット(scree plot)は、各因子の固有値を降順に折れ線グラフにしたもの。平たく言えば、固有値は抽出した因子の持つ情報量を表している。固有値が大きい順に並べると、意味の薄い潜在因子は追加しても折れ線が横ばいに近くなる。「折れ線が急激に下がったところまで含める」という基準はかなり曖昧で、どこまで相関行列に含まれる誤差の影響があるのかも分からない。
そこで、データと同じサンプルサイズの乱数を発生させて、その乱数同士の相関行列の固有値を求め、スクリープロットと重ねて判断する。これが平行分析で、fa.parallel()を使って実装する。
主な引数は以下のとおり。
- 第一引数:データもしくは相関行列。下のコードでは欠測を除外したデータでの相関行列を入力した。
n.obs:データ数。この数と同じ数の乱数を発生させる。ここでは欠測を除外して相関行列を計算しているので、結束を除外した例数を与える。n.iter:シミュレーションの回数fm:推定方法。最小残差法("minres")がデフォルト。これか最尤法("ml")を使うとよい。fa:主成分分析と因子分析のどちらを用いるか。
fa.parallel(cor(data, use="na.or.complete"), n.obs=nrow(na.omit(data)), n.iter=50, fm="minres", fa="both")
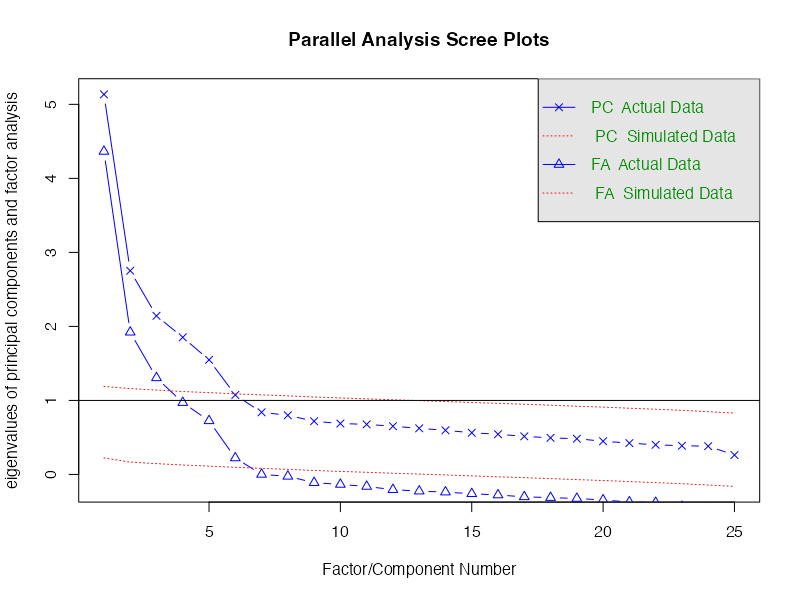
赤線が乱数、青線が実データ。青線で示された実データの固有値が赤線を上回る因子を選ぶ。グラフから大小が読み取りにくいときは、
fp <- fa.parallel(x) fp$fa.values
などとして、実際の数値を取り出す。
$fa.value:実データの因子分析の固有値$fa.sim:シミュレーションデータの因子分析の固有値$pc.value:実データの主成分分析の固有値$pc.sim:シミュレーションデータの主成分分析の固有値
コンソールには、FAなら6因子、PCAなら5因子が推奨と表示された。
Parallel analysis suggests that the number of factors = 6 and the number of components = 5
因子分析を用いた平行分析で提案される因子数が最も多い。これ以上の因子数は用いないように。主成分分析を用いた平行分析で提案される因子数もまあまあ良いみたいだが、なぜEFAなのにPCAの結果が参考になるのかは理解できず。
3. 因子の抽出
fa( )を使って因子負荷を推定する。指定する主な引数は次のとおり。
- 第一引数:データもしくは相関行列
use:欠測の扱い方。cor()で指定できるものが選択肢で、"pairwise"がデフォルト。nfactors:因子数。決め方は前述のとおり。fm:推定方法。デフォルトは"minres"(最小残差法)。サンプルサイズが大きいなら"ml"(最尤法)を使うべきとのこと。rotate:因子軸の回転方法。おすすめはデフォルトの"oblimin"(オブリミン回転)とのこと(後述)。
result <- fa(data, use = "complete.obs", nfactors = 5, fm = "ml", rotate = "oblimin")
結果の表示は後述。
4. 因子軸の回転
各項目の因子負荷が特定の因子に大きな値を持ち、それ以外はゼロに近い方が解釈しやすい。 解釈しやすくなるように因子軸を回転させるのだが、その回転のさせ方にも色々ある。
直交回転と斜交回転
直交回転とは、因子間に相関がないことを想定した回転方法。でも通常は相関があるので、まずは斜交回転を用いる方が当てはまりがよい。前述のfa( )の引数rotateで指定する。
直交回転で選べるもの:
- "varimax":バリマックス回転
- "quartimax":クオーティマックス回転
- "geominT":ジオミン直交回転
斜行回転で選べるもの:
- "promax":プロマックス回転。簡便なのでよく使われる必ずしも良い方法ではないらしい。
- "cluster":独立クラスター回転。各項目に1因子しか負荷しない状態を目指す。
- "oblimin":オブリミン回転。fa()のデフォルトなので、基本的にこれでいいと思う。
- "geominQ":ジオミン斜交回転
5. 結果の解釈
「3. 因子の抽出」で推定した因子構造の結果をprint()で表示したものを順に確認していく。以下、見やすく表示するための引数。
digits:小数第何位まで表示するか。cut:因子負荷量(factor loading)がこれよりも小さいものは表示しない。sort:影響力の大きい潜在因子および項目の順に並べ替えて表示。
print(result, digits=2, cut=0.3, sort=TRUE)
因子負荷量(factor loading)
Factor Analysis using method = ml Call: fa(r = data, nfactors = 5, rotate = "oblimin", fm = "ml", use = "complete.obs") Standardized loadings (pattern matrix) based upon correlation matrix item ML2 ML5 ML3 ML1 ML4 h2 u2 com N1 16 0.87 0.73 0.27 1.0 N2 17 0.82 0.66 0.34 1.0 N3 18 0.66 0.52 0.48 1.2 N5 20 0.44 0.34 0.66 2.4 A3 3 0.69 0.53 0.47 1.0 A2 2 0.63 0.42 0.58 1.0 A5 5 0.58 0.49 0.51 1.3 A4 4 0.47 0.31 0.69 1.6 A1 1 -0.39 0.17 0.83 1.9 C4 9 -0.67 0.49 0.51 1.1 C2 7 0.64 0.43 0.57 1.2 C5 10 -0.58 0.44 0.56 1.3 C3 8 0.57 0.32 0.68 1.1 C1 6 0.54 0.34 0.66 1.2 E2 12 0.65 0.55 0.45 1.1 E1 11 0.56 0.37 0.63 1.3 E4 14 0.36 -0.54 0.53 0.47 1.7 N4 19 0.41 0.44 0.49 0.51 2.4 E5 15 -0.39 0.41 0.59 3.1 E3 13 -0.34 0.33 0.44 0.56 3.0 O3 23 0.64 0.48 0.52 1.1 O1 21 0.54 0.33 0.67 1.0 O5 25 -0.52 0.27 0.73 1.2 O2 22 -0.46 0.26 0.74 1.8 O4 24 0.36 0.37 0.25 0.75 2.4
行方向にN1〜O4の25個の観察項目(観察変数)が並び、それぞれの項目に対する因子負荷量などが列方向に表示されている。
ここでは5つの因子にML1からML5の名前が振られている。今は最尤法(method="ml")を指定したので"ML"が接頭辞になっている。ちなみにmethod="minres"とすると"MR"になった。
それぞれの因子の列(ここではML1〜5)に記載されている数値が因子負荷量(factor loading)で、-1から+1の値を取る。絶対値が1に近いほど、観察項目と因子の関係性が強い。目安としては、絶対値が0.6以上なら高く、0.3未満なら低い。上記では見やすさのためcut=0.3としたので、絶対値が0.3未満の数値は表示されない。
h2は共通性(communality)で、潜在因子で説明される分散の割合を示している。
u2は独自分散(unique variance)で、共通の潜在因子で説明されない分散の割合を表している。
両者を足すと1になるようになっている。
comは複雑性(complexity)で、1に近いほど単純構造(観察項目がたった1つの因子で説明される)に近い。
因子寄与・因子寄与率・累積因子寄与率
ML2 ML5 ML3 ML1 ML4 SS loadings 2.50 2.17 2.11 2.10 1.69 Proportion Var 0.10 0.09 0.08 0.08 0.07 Cumulative Var 0.10 0.19 0.27 0.36 0.42 Proportion Explained 0.24 0.21 0.20 0.20 0.16 Cumulative Proportion 0.24 0.44 0.64 0.84 1.00
SS loadings(因子寄与):各因子が観察変数の変動をどの程度説明しているか。各因子ごとに因子負荷量の2乗の総和を取ったもの。Proportion Var(因子寄与率):各因子の因子寄与を観察項目の個数で割ったもの。直交回転では因子寄与の合計は観察変数の個数になるから観察項目を分母にした*2。Cumulative Var(累積因子寄与率):因子寄与率を大きい方(第1因子)から累積していったもの。Proportion Explained(説明率):因子寄与率の総和に対する割合。例えば、因子寄与率の総和(=累積因子寄与率の最大値)は0.42なので、"ML2"では因子寄与率0.1を0.42で割った0.238≒0.24となっているCumulative Proportion(累積説明率):上記の累積率。
因子間相関
With factor correlations of
ML2 ML5 ML3 ML1 ML4
ML2 1.00 -0.04 -0.21 0.24 0.00
ML5 -0.04 1.00 0.20 -0.32 0.23
ML3 -0.21 0.20 1.00 -0.23 0.20
ML1 0.24 -0.32 -0.23 1.00 -0.17
ML4 0.00 0.23 0.20 -0.17 1.00
Mean item complexity = 1.6
直交回転のときは因子間に相関がないことを仮定しているので、因子間相関は表示されない。 全体の複雑性も表示されている。
適合度指標
Test of the hypothesis that 5 factors are sufficient. The degrees of freedom for the null model are 300 and the objective function was 7.48 with Chi Square of 20868.91 The degrees of freedom for the model are 185 and the objective function was 0.62 The root mean square of the residuals (RMSR) is 0.03 The df corrected root mean square of the residuals is 0.04 The harmonic number of observations is 2762 with the empirical chi square 1356.93 with prob < 2.4e-177 The total number of observations was 2800 with Likelihood Chi Square = 1714.56 with prob < 1e-245 Tucker Lewis Index of factoring reliability = 0.879 RMSEA index = 0.054 and the 90 % confidence intervals are 0.052 0.057 BIC = 246.14 Fit based upon off diagonal values = 0.98 Measures of factor score adequacy ML2 ML5 ML3 ML1 ML4 Correlation of (regression) scores with factors 0.93 0.89 0.88 0.89 0.85 Multiple R square of scores with factors 0.87 0.79 0.78 0.78 0.72 Minimum correlation of possible factor scores 0.74 0.58 0.56 0.57 0.45
カイ2乗値, RMSR, Tucker Lewis Index, RMSEA, BICなどの適合度指標が表示されている(説明は別の機会に)。
fa.diagram( )でパス図を描く
fa( )で推定した結果をfa.diagram( )に渡してパス図を描くことができる。
cut:表示する数値の下限simple:TRUEとすると各観察項目で最も関連の強い因子からだけ矢印が引かれるsort:TRUEとすると各因子に関係のある観察変数を因子負荷量順に並べ替えるerrors:TRUEとすると独自因子を表す矢印を追加
fa.diagram(result, digits = 2, cut = 0.3, sort = TRUE, simple = TRUE, errors = FALSE, main = "Factor Diagram")
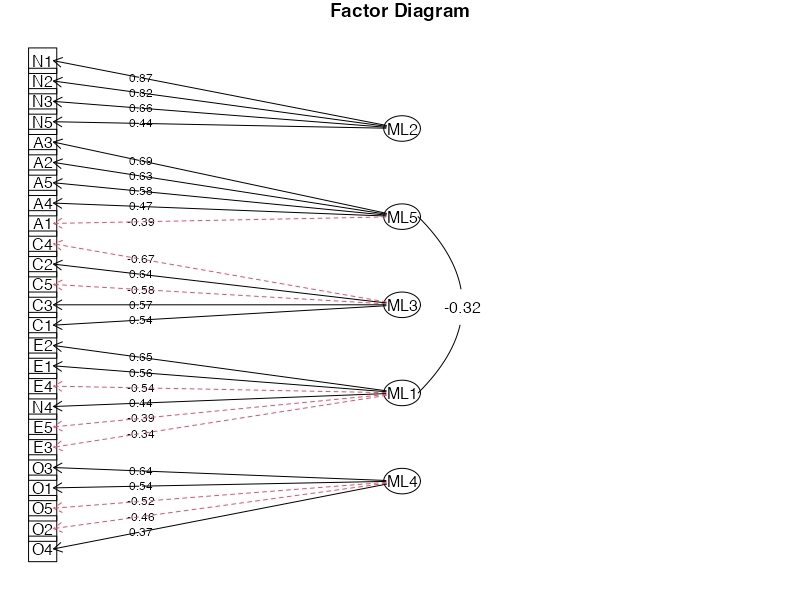
因子負荷量がマイナスのものは赤・点線で描かれる。
おわりに
- 質問紙研究は苦手ですが、アンケートに答えるのは結構好きです。
参考資料
- 津田裕之先生が公開している資料です。因子分析の手順がわかりやすく説明されています。
- 清水裕士先生のslideshareです。
- 清水裕士先生による因子数選択についての解説。
George M Harrison. Using R for Measurement in the Social Sciences. Chapter 12 Exploratory Factor Analysis.
psychパッケージを使った因子分析の結果の見方についてまとめて下さってます。
- データに欠測があるときの相関係数については、下のブログが詳しくまとめてくださっています。
*1:https://htsuda.net/stats/factor-analysis.html
*2:直交回転なら回転させて、ある因子に対する因子負荷量が高くなっても、その分他の因子の因子負荷量が低下するので因子寄与の最大値が計算可能。斜交回転ではどの因子に対しても高い因子負荷量を示すようにすることが可能なので最大値が定まらず、相対的な比較にとどまる。