高校生のためのデータ分析入門 (14)：2つの変数の間には相関がある？

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (13)：分散を計算しよう - ねこすたっと

相関ってなに？
相関係数ってなに？
- 相関係数が意味するものを図で考えてみよう
- 相関係数を解釈する
相関係数を解釈するときの注意
おわりに

相関ってなに？

相関（correlation）は、2つの変数において一方が増えると他方も直線的に増える（あるいは減る）ような関係にあること、と説明されます。一般的に色々な状況・分野で使われる用語なので、これで間違いではないんですが、統計学においては相関係数で定義される狭い意味の言葉として理解しておく方がいいです（つまり、相関係数をつけずして、「相関がある・ない」みたいな話はしない方がよい、ということ）。

相関係数ってなに？

相関係数（correlation coefficient）は、対をなす2つの連続変数X, Yの相関の強さを表します。「対をなす」というのはペアを作っている、という意味で、例えば、X=身長、Y=同じ人の体重、のような変数の組です。ペアを作っているデータなので、XもYも同じ数（n個）だけあります。

相関係数*1は下の式で表されます。

$\begin{aligned} r &= \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}} \\ &= \frac{E[(X-E[X])(Y-E[Y])]}{\sqrt{E[(X-E[X]^2)]E[(Y-E[Y]^2)]}} \end{aligned}$

ここで、分母はXとYの標準偏差の積、分子はXとYの共分散（covariance）です。分散は、ある変数について平均からの距離の2乗を足し合わせたものでした。共分散は、2つの変数について、それぞれの平均からの距離の積を足し合わせたものです。

実際の計算はどうなるでしょうか。変数X, Yの平均をそれぞれ $\bar{X}, \bar{Y}$ とすると、

$\begin{aligned} r &= \frac{\frac{\sum_i^n (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}}{\sqrt{\frac{\sum_i^n (X_i - \bar{X})^2 }{n-1}\frac{\sum_i^n(Y_i - \bar{Y})^2}{n-1}}} \\ &= \frac{\sum_i^n (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_i^n (X_i - \bar{X})^2 \sum_i^n(Y_i - \bar{Y})^2}} \end{aligned}$

となります。共分散も、「nで割るか・n-1で割るか問題」がありますが、分母と分子に同じものが登場することになるので、どちらを使っても同じ値が計算されます。

相関係数が意味するものを図で考えてみよう

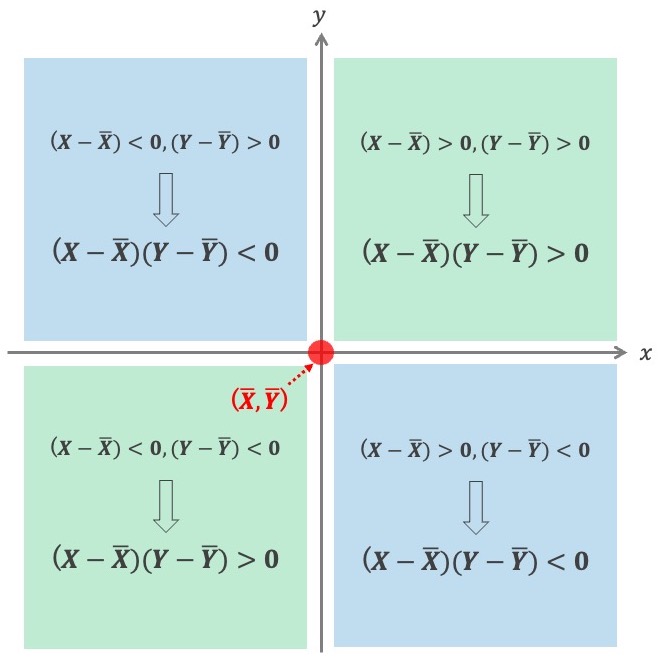
まずは分子である共分散がどのように決まってくるか、見てみましょう。下の図は、X, Yの平均を中心としたx-y座標平面です。

観測値が右上のエリアに入る場合、 $X_i - \bar{X}$ も $Y_i - \bar{Y}$ も正になるので、その積も正になります。左下のエリアに入った場合は、両方とも負になるので、このときも積は正になります。左上と右下の場合は、 $X_i - \bar{X}$ と $Y_i - \bar{Y}$ の一方が正で他方が負になるので、積は負になりますね。

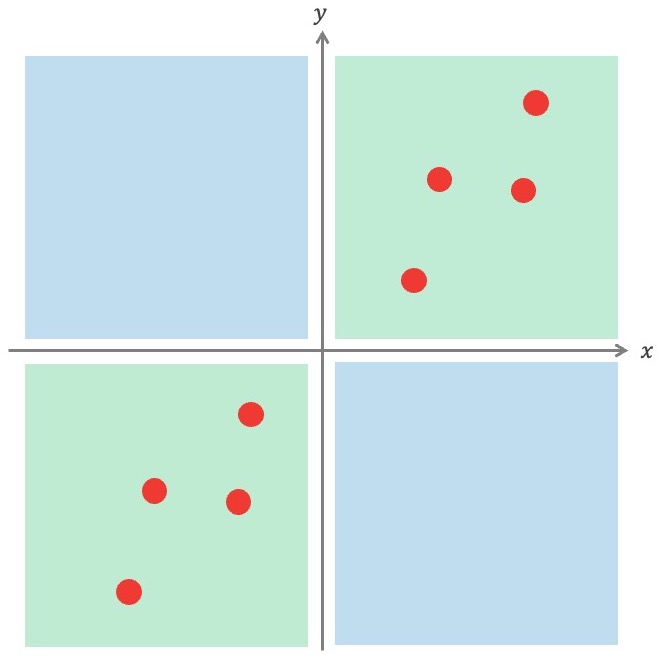
もし、観察されたデータにおいて、積>0のエリア（緑）に入るものばっかりだったら、相関係数は正になりますよね。

一部のデータが積<0のエリア（青）に入ってくると、その分、総和は小さくなります。

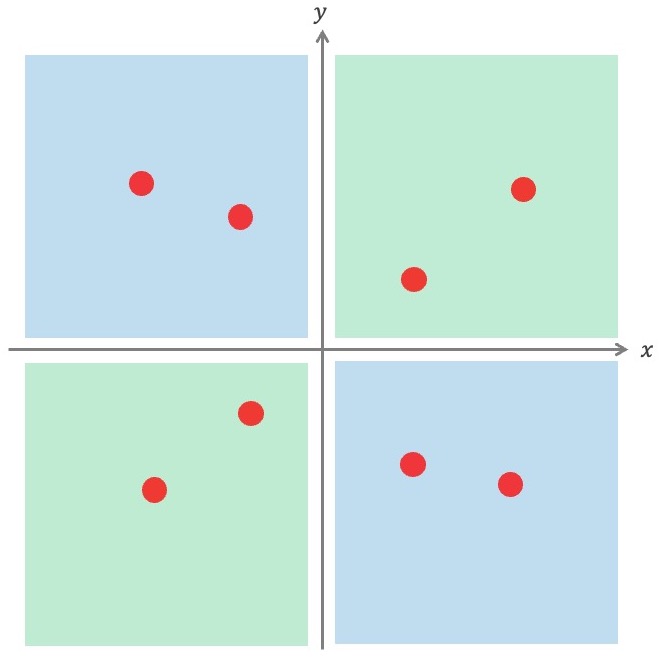
さらに積<0のエリア（青）に入るものが増えて均等になってくると、打ち消しあって総和が0近辺になります。

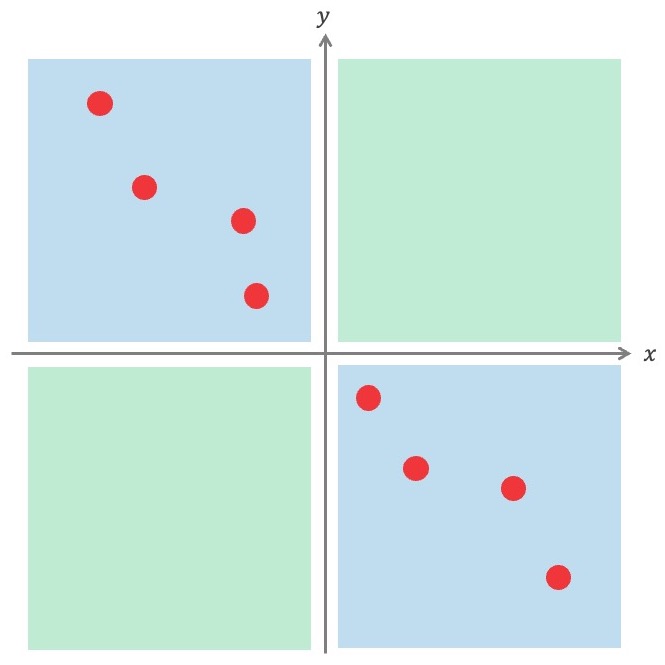
さらにさらに積<0のエリア（青）に入るのが増えると、総和は負になります。

このことから、共分散について次のことが分かります。

分散と違って、共分散は負になることがある。
データが右肩上がりに並べは正、右肩下がりに並べば負になる。
データが直線的に並べは並ぶほど、共分散の絶対値は大きくなる。

このままだと１つ困ったことがあります。平均からの距離が大きいデータほど、共分散の絶対値は大きくなってしまうので、共分散が大きくても、直線的関係が強いからなのか、データのバラツキが大きいからなのか、判断できないのです。

そこで、それぞれの変数の分散で割ることで、後者の影響を取り除きます。分子と分母の次数を揃えた方がキレイなので、分母は平方根を取ることにしましょう。こうして出来たのが相関係数です。

相関係数を解釈する

共分散を分散で補正した結果、相関係数は-1〜+1の範囲に収まります。

相関係数の正負は、関係性が右肩上がりなのか、右肩下がりなのかを示します。

r>0のとき「XとYの間には正の相関関係がある」
r<0のとき「XとYの間には負の相関関係がある」
r=0のとき「XとYの間には相関関係はない」

相関係数の絶対値は、直線的関係性の強さを示します。慣例的な目安として、

| r | = 0.7〜1.0のとき「強い相関関係がある」
| r | = 0.4〜0.7のとき「やや相関関係がある」
| r | = 0.2〜0.4のとき「弱い相関関係がある」
| r | = 0.0〜0.2のとき「ほとんど相関関係はない」

と表現します。下の図は、Wikipedia - 相関係数からお借りしました。相関係数と実際の散布図でどのように見えるかがよくわかりますね。

相関係数を解釈するときの注意

P値を気にしすぎない

ときどき（というかしばしば）相関係数の横にP値が書かれていることがあります。これは「相関係数が0である」という仮定のもとで手元のデータが得られる確率を表しています。

例えば、r=0.1, P<0.001という結果が得られたとしましょう。P値だけを見れば「統計的有意な相関関係があった」と言いたくなるところですが、相関係数はとても小さく、「ほとんど相関関係はない」と解釈する方が適切です。サンプル数が多くなれば、ほとんどの場合でP値は十分小さくなるので、P値だけで語るのは意味がないんです。