構造方程式モデリング(Structural Equation Modeling, SEM)の初学者が、 タイトルの "Handbook" に誘われて買ってしまったHoyle先生の分厚い本を拾い読みしたメモです。 といっても、私にとって重すぎる内容は拾い上げられていません。
今回は "Chapter 22:Confirmatory Factor Analysis" から。 これまでもCFAについてまとめたことがありますが、実装方法が中心だったので、今回は教科書で学び直しです。
- 因子分析(factor analysis, FA)とは
- CFAモデルに含まれるパラメータ
- パラメータ推定値の測定単位系
- モデルから計算される分散・共分散の推定値
- 推定結果で確認してみる
- モデルの評価
- おわりに
因子分析(factor analysis, FA)とは
複数の観測変数(indicator)から潜在的な共通性を因子(factor)として抽出することを目的としています。観測変数の分散を、共通因子によって説明される部分(共通分散, common variance)と、個々の観測変数に固有の部分(独自分散, unique variance)に分ける ことで、因子-観測変数関係(factor-indicator relationship)を見ようとする解析です。
FAには次の2種類があります。
探索的因子分析(exploratory FA, EFA):
- 因子の数や因子-観測変数間の関係性を事前に設定しない
- 探索的・記述的
- 測定誤差同士は独立しているという仮定が必要
- 最大の因子負荷を1、最小の因子負荷を0に近づけるように回転させる
検証的因子分析(confirmatory FA, CFA):
- 研究者が先行研究やその領域の知見・経験をもとにして、因子の数や因子-観測変数間の関係性を事前に設定する
- 事前の経験的・理論的背景を確立するために行われる
- 測定誤差同士に相関関係があっても良い
- 因子負荷は回転させない
CFAは理論的に構築されたモデルの妥当性検証に必要不可欠な解析ツールです。 理論的に類似していると考えられる観測変数の相関が強いことを確かめたり(convergent validity)、逆に理論的に異なっていると考えられる観測変数間の相関がそれほど高くないことを確かめたり(discriminant validity)するのに使われます。
他にも、ある測定モデルが地理的・文化的に異なった集団においても同じように用いることができるかを評価する際にも用いられます。
SEMは事前にモデルを設定するのでEFAとは別物です。ここではCFAのみ扱います。
CFAモデルに含まれるパラメータ
下のパス図は2因子6項目のCFAの例です。
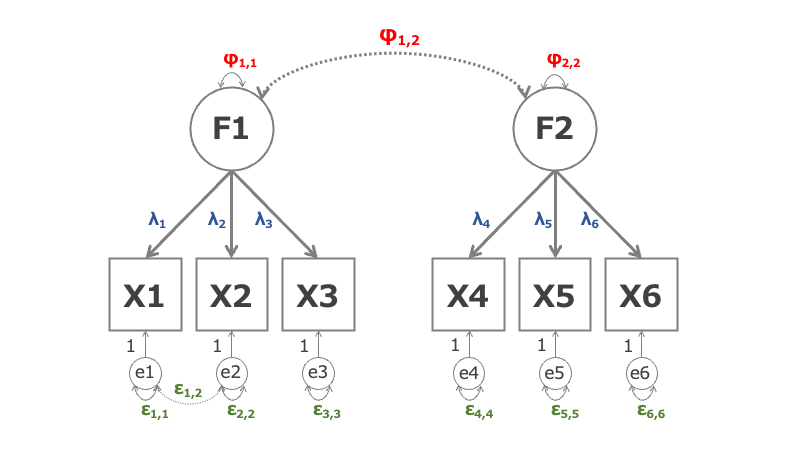
CFAに含まれるパラメータは、
- 因子負荷量(factor loading):因子が観測変数に与える影響の度合い(
)
- 独自分散(unique variance):各観測変数に固有に与えられた独自因子の分散(
)
- 共通分散(common variance):因子の分散(
)
があります。これらに加えて、
- 因子間共分散
(covariance between factors)
- 誤差間共分散
(error covariance)*1
を設定することができます。
パラメータ推定値の測定単位系
潜在変数には測定単位がないので、何らかの制約(単位基準)を設ける必要があります。
方法1:変数を標準化する方法
変数の分散を1に固定する方法です。これを標準化(standardized)*2と言います。
潜在変数・観測変数の両方を標準化する場合をcompletely standardization、片方だけを標準化する場合をpartially standardizationと呼びますが、とりあえず前者を知っていれば事足りそうです。
方法2:マーカー変数法
それぞれの因子に属する観測変数のうち、1つの変数の因子負荷量を1に固定する方法です。方法1に対して、こちらでは変数は必ずしも標準化されていません(unstandardized)。
モデルから計算される分散・共分散の推定値
モデルが正しいという仮定のもとでは、目的の観測変数間の経路で因子負荷量と因子の分散を掛け合わせていくことで求められます。例えば、
同じ因子内の観測変数の共分散は、
異なった因子内の観測変数の共分散は、
となります。
観測変数の誤差間に相関がある場合は、誤差間の共分散を足します。
この式で2つの変数を同じにすると、 観測変数の分散が属する因子の共通分散と独自分散の和になることが導かれます。
一方、観測されたデータからは、
- 個々の観測変数の分散
- 観測変数間の共分散
が得られます。 モデルが正しいという仮定のもとでパラメータを使って表した分散・共分散と、実際に観測された分散・共分散を比べることでパラメータを推定していきます。
推定結果で確認してみる
以前lavaanパッケージでCFAを実行する方法をまとめたときと、同じ例を使って推定結果を確認してみます。
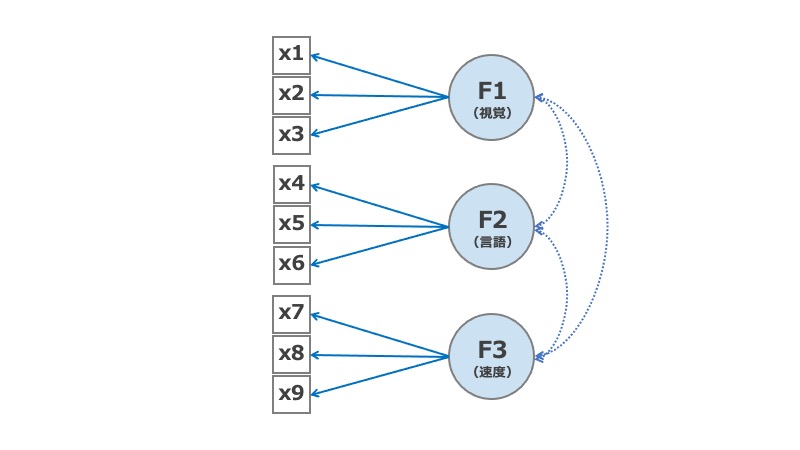
# パッケージとデータの準備 library(lavaan) data <- HolzingerSwineford1939[-c(1:6)]
まずは使用するデータの共分散行列を見てみます。
> round(cov(data),digits=3) x1 x2 x3 x4 x5 x6 x7 x8 x9 x1 1.363 0.409 0.582 0.507 0.442 0.456 0.085 0.265 0.460 x2 0.409 1.386 0.453 0.210 0.212 0.248 -0.097 0.110 0.245 x3 0.582 0.453 1.279 0.209 0.113 0.245 0.089 0.213 0.375 x4 0.507 0.210 0.209 1.355 1.101 0.899 0.220 0.126 0.244 x5 0.442 0.212 0.113 1.101 1.665 1.018 0.143 0.181 0.296 x6 0.456 0.248 0.245 0.899 1.018 1.200 0.145 0.166 0.237 x7 0.085 -0.097 0.089 0.220 0.143 0.145 1.187 0.537 0.375 x8 0.265 0.110 0.213 0.126 0.181 0.166 0.537 1.025 0.459 x9 0.460 0.245 0.375 0.244 0.296 0.237 0.375 0.459 1.018
相関係数rと共分散Covの関係は、
なので、共分散行列で変数を標準化したものは相関行列になります。
> round(cor(data),digits=3) x1 x2 x3 x4 x5 x6 x7 x8 x9 x1 1.000 0.297 0.441 0.373 0.293 0.357 0.067 0.224 0.390 x2 0.297 1.000 0.340 0.153 0.139 0.193 -0.076 0.092 0.206 x3 0.441 0.340 1.000 0.159 0.077 0.198 0.072 0.186 0.329 x4 0.373 0.153 0.159 1.000 0.733 0.704 0.174 0.107 0.208 x5 0.293 0.139 0.077 0.733 1.000 0.720 0.102 0.139 0.227 x6 0.357 0.193 0.198 0.704 0.720 1.000 0.121 0.150 0.214 x7 0.067 -0.076 0.072 0.174 0.102 0.121 1.000 0.487 0.341 x8 0.224 0.092 0.186 0.107 0.139 0.150 0.487 1.000 0.449 x9 0.390 0.206 0.329 0.208 0.227 0.214 0.341 0.449 1.000
次にCFAモデルを設定してパラメータを推定します。
# 使用するCFAモデル model = " F1 =~ x1 + x2 + x3 F2 =~ x4 + x5 + x6 F3 =~ x7 + x8 + x9 " # 標準化した場合 fit_std <- cfa(model = model, data=data, estimator = "MLR", std.lv=TRUE) # 標準化しない場合 fit_unstd <- cfa(model = model, data=data, estimator = "MLR", std.lv=FALSE, auto.fix.first = TRUE)
結果1:潜在変数を標準化した場合
確認に使うところ以外は省略してます。
summary(fit_std, fit.measures=TRUE, standardized=TRUE)
~~~~~(省略)~~~~~ Latent Variables: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 =~ x1 0.900 0.100 8.973 0.000 0.900 0.772 x2 0.498 0.088 5.681 0.000 0.498 0.424 x3 0.656 0.080 8.151 0.000 0.656 0.581 F2 =~ x4 0.990 0.061 16.150 0.000 0.990 0.852 ~~~~~(省略)~~~~~ Covariances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 ~~ F2 0.459 0.073 6.258 0.000 0.459 0.459 ~~~~~(省略)~~~~~ Variances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all .x1 0.549 0.156 3.509 0.000 0.549 0.404 .x2 1.134 0.112 10.135 0.000 1.134 0.821 .x3 0.844 0.100 8.419 0.000 0.844 0.662 .x4 0.371 0.050 7.382 0.000 0.371 0.275 ~~~~~(省略)~~~~~ F1 1.000 1.000 1.000 F2 1.000 1.000 1.000 F3 1.000 1.000 1.000
(1) まずは観測変数の分散についてです。
- F1-x1の因子負荷量 = 0.900(← Latent Variablesに記載)
- F1の分散 = 1.000(← Variancesに記載)
から、x1の共通分散の推定値は0.900 × 1.000 × 0.900 = 0.810となります。
また、Variancesに記載されている.x1はx1の独自分散の推定値で0.549です。
両者を足すと0.810 + 0.549 = 1.359となり、x1の分散1.363に近い数値になっているので、推定値としてはまずまず良さそうです(過剰識別のモデルで再現性が悪ければかけ離れた数値になる)。
(2) 次に同じ因子に属する観測変数(x1, x2)の共分散です。
- F1-x1の因子負荷量 = 0.900
- F1の分散 = 1.000
- F1-x2の因子負荷量 = 0.498
から、Cov(x1,x2)の推定値 = 0.900 × 1.000 × 0.498 = 0.448となります。実際の値は0.409ですのでまずまず良い推定値に見えます。
(3) 最後に異なった因子に属する観測変数(x1, x4)の共分散です。
- F1-x1の因子負荷量 = 0.900
- F1-F2の共分散 = 0.459
- F2-x4の因子負荷量 = 0.990
なので、Cov(x1,x4)の推定値 = 0.900 × 0.459 × 0.990 = 0.409となります(実際の値は0.507でした)。
結果2:マーカー変数の因子負荷量を1に固定した場合
次にマーカー変数法(方法2)の場合です。
summary(fit_unstd, fit.measures=TRUE, standardized=TRUE)
~~~~~(省略)~~~~~ Latent Variables: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 =~ x1 1.000 0.900 0.772 x2 0.554 0.132 4.191 0.000 0.498 0.424 x3 0.729 0.141 5.170 0.000 0.656 0.581 F2 =~ x4 1.000 0.990 0.852 ~~~~~(省略)~~~~~ Covariances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all F1 ~~ F2 0.408 0.099 4.110 0.000 0.459 0.459 ~~~~~(省略)~~~~~ Variances: Estimate Std.Err z-value P(>|z|) Std.lv Std.all .x1 0.549 0.156 3.509 0.000 0.549 0.404 .x2 1.134 0.112 10.135 0.000 1.134 0.821 .x3 0.844 0.100 8.419 0.000 0.844 0.662 .x4 0.371 0.050 7.382 0.000 0.371 0.275 ~~~~~(省略)~~~~~ F1 0.809 0.180 4.486 0.000 1.000 1.000 F2 0.979 0.121 8.075 0.000 1.000 1.000 F3 0.384 0.107 3.596 0.000 1.000 1.000
先程と同じ内容を確認してみます。
(1) まずは観測変数の分散についてです。
- F1-x1の因子負荷量 = 1.000(← Latent Variablesに記載)
- F1の分散 = 0.809(← Variancesに記載)
なので、x1の共通分散の推定値は1.000 × 0.809 × 1.000 = 0.809となります。標準化したときの値0.810とほぼ同じです(ズレは丸めの影響でしょう)。
(2) 次に同じ因子に属する観測変数(x1, x2)の共分散です。
- F1-x1の因子負荷量 = 1.000
- F1の分散 = 0.809
- F1-x2の因子負荷量 = 0.554
から、Cov(x1,x2)の推定値 = 1.000 × 0.809 × 0.554 = 0.448となり、標準化したときと同じ値になりました。
(3) 最後に異なった因子に属する観測変数(x1, x4)の共分散です。
- F1-x1の因子負荷量 = 1.000
- F1-F2の共分散 = 0.408
- F2-x4の因子負荷量 = 1.000
なので、Cov(x1,x4)の推定値 = 1.000 × 0.408 × 1.000 = 0.408で、標準化したときの値0.409と同じ値です。
寄与率
Std.lvは潜在変数(lv = latent variable)のみ標準化した結果、Std.allは観測変数も標準化した結果です。
ここで再々度、観測変数の分散についてです。
結果1でStd.allの値を使うと、F1-x1の因子負荷量 = 0.772なので、 x1の共通分散は0.772 × 1.000 × 0.772 = 0.596です。 x1の独自分散は0.404なので、両者の和は0.596 + 0.404 = 1となり、観測変数についても標準化されていることが確認できました。
ここで、分散全体に対する共通分散の割合(=0.596)は寄与率と呼ばれ、x1の変動のうち59.6%が因子F1によって説明されることを示しています。
モデルの評価
設定したモデルを使ってパラメータが推定できたら、以下の3点について評価します。項目を挙げるだけなので、詳細は成書で確認してください。
- モデル全体の当てはまり
- モデル局所の当てはまり
- パラメータ推定値の解釈
設定したモデルがイマイチだった場合、因子数や変数同士の関係性を見直すことがあります(respecification)。
モデル全体の当てはまり
値で評価すると、サンプル数が多いときにほとんど必ず有意差が出てしまう(つまり、モデルのデータがずれている)という問題があるそうです。
なので、他にも次のような指標を使って評価します。
- standardized root mean square residual(SRMR):<0.08ならOK
- root mean square error of approximation(RMSEA):<0.06ならOK
- Tucker-Lewis index(TLI):>0.95ならOK
- comparative fit index(CFI):>0.95ならOK
モデル局所の当てはまり
全体の当てはまりが良くても、ある観測変数については再現性がよくないことがあります。次の指標を追加います。
- standardized residuals:>1.96だとズレが大きい
- modification index:パラメータに関する制約を外したときに
値がどれくらい変化すうるか。df=1の
値が3.84なので、これを超えて低下する場合はパラメータに関する制約が誤っているかもしれない。
パラメータ推定値の解釈
あくまでモデルの当てはまりが良いことが前提条件です。 次の項目を確認します。
- パラメータが取りうる範囲に収まっているか
- 大きさ・方向が概念上・経験上の観点から説明可能か
- 因子間の相関が大きすぎないか。1に近いときは、因子で重複している要素が多いことになる。
おわりに
- CFAの章を読んで、少しSEMに対する苦手意識が和らぎました。最初にこの章を読めばよかったです。
- なぜか数式のフォントが変です。どうしたら直るのでしょうか。(→追記:公開したら直りました)
- 猫が布団に潜り込んでこなくなって春の訪れを感じました。
