Cox比例ハザードモデルを当てはめてadjusted survival curveを描く（ggplot系survminerパッケージ）[R]

パッケージとデータの準備
Coxモデルへ当てはめる
ggadjustedcurves( )を使ってadjusted survival curveを描く
- 群間で患者背景を揃えた生存曲線
- 新規患者に期待される生存曲線
おわりに
参考資料

Cox比例ハザードモデル（Cox proportional hazard model, CPH model）は生存時間データに対するモデルとして（多分）最も用いられている。
このモデルにおいては、ハザード関数 $h(X,t)$ *1が以下のように表されると仮定する。

$h(X,t) = h_0(t) e ^{\Sigma \beta X}$

$h_0(t)$ は時間tに依存するが共変量Xには依存しない部分で、ベースラインハザード関数と呼ばれる。
$e ^{\Sigma \beta X}$ は共変量Xに依存するが時間tには依存しない部分。指数変換しているのはハザード関数が負にならないようにするため。
ベースラインハザード関数の部分は特定しないので、セミパラメトリックモデルと言われる。

変数xが $x_1, x_2$ の2つの集団におけるハザード関数は、

$h(x=x_1,t) = h_0(t) \times e ^{\beta_0 + \beta_1 x_1} \\ h(x=x_2,t) = h_0(t) \times e ^{\beta_0 + \beta_1 x_2}$

となる。
ハザード比を取ると、

${\displaystyle \frac{h(x=x_1,t)}{h(x=x_2,t)} = e^{\beta_1 (x_1 - x_2)} = e^{\beta \Delta x} }$

ベースラインハザードや同じ値の変数は打ち消されるので、係数βの指数変換 $e^{\beta}$ は調整後ハザード比として解釈できる。

パッケージとデータの準備

まずは必要なパッケージを準備する。

library(survival)
library(survminer)
library(ggplot2)
library(tidyverse)

ここではsurvivalパッケージ内のveteranデータセットを使う。
これは退役軍人を対象とした肺癌治療のRCTのデータ。ラベルを付け直して使用する。

d <- veteran %>% 
  mutate(age_cat = if_else((age<60),"under60","over60"),
  age_cat = factor(age_cat),
  trt = factor(trt, labels=c("standard","test")),
  prior = factor(prior, labels=c("N","Y")))

> head(d,3)
       trt celltype time status karno diagtime age prior age_cat
1 standard squamous   72      1    60        7  69     N  over60
2 standard squamous  411      1    70        5  64     Y  over60
3 standard squamous  228      1    60        3  38     N under60

使用する変数は以下のもの。

trt：治療群（"standard" vs. "test"）
celltype：病理型（"squamous", "smallcell", "adeno", "large"）
age_cat：年齢カテゴリー（"under60", "over60"）
prior：先行治療（"Y", "N"）

Coxモデルへ当てはめる

survivalパッケージのcoxph( )を使う。

fit <- coxph(Surv(time, status) ~ trt + celltype + age_cat + prior, data=d)

結果はsummary( )やbroomパッケージのtidy( )で取り出せばよい（後者のみ表示）。

> library(broom)
> tidy(fit, exponentiate=TRUE, conf.int=TRUE)
# A tibble: 6 x 7
  term              estimate std.error statistic  p.value conf.low conf.high
  <chr>                <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 trttest              1.18      0.197     0.840 0.401       0.802      1.74
2 celltypesmallcell    2.86      0.275     3.82  0.000135    1.67       4.89
3 celltypeadeno        3.14      0.300     3.81  0.000139    1.74       5.65
4 celltypelarge        1.29      0.286     0.899 0.368       0.738      2.27
5 age_catunder60       0.803     0.194    -1.13  0.260       0.549      1.18
6 priorY               1.05      0.206     0.238 0.812       0.701      1.57

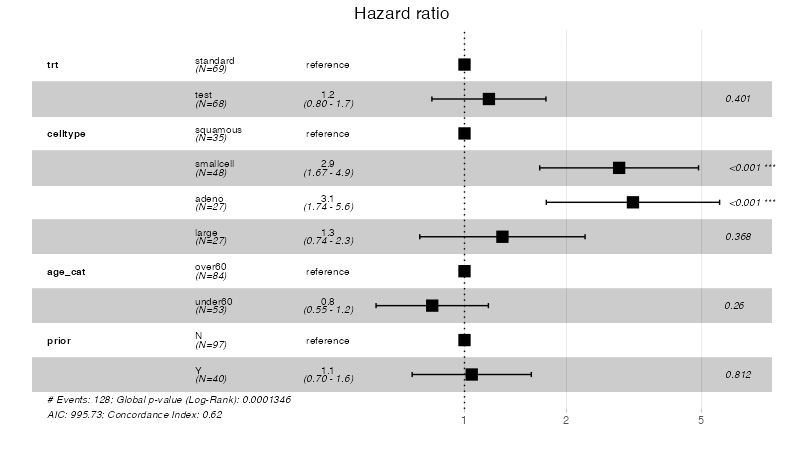
ggforest( )を使うと簡単にforest plotを表示できる。

ggforest(fit, data=d)

ggadjustedcurves( )を使ってadjusted survival curveを描く

推定したCoxモデルを使って、共変量が任意の値のときの生存曲線を描くことができる。
これを使えば、

比較したい群間の患者背景を揃えた状態で生存曲線を描く
新規患者（あるいは集団）の特性に基づいて期待される生存曲線を描く

などができる。

群間で患者背景を揃えた生存曲線

患者背景の調整方法にはmarginal approach（standardizationやweighting）やconditional approach（stratificationやmodeling）がある。
ggadjustedcurves( )では以下の変数で調整方法を指定できる。

data：生存曲線を描きたい対象集団（指定なければCoxモデルを当てはめるときに使ったデータが使われる）
variable：層別に描き分ける変数
method：
- "single"：集団全体で期待される生存曲線を1本だけ描く
- "average"：各層ごとの平均生存曲線を描く（層ごとの対象者の違いは均衡化しない）
- "marginal：各層の患者背景をreferenceで指定した集団と同じに揃えて生存曲線を描く（IPWを使っているみたい）
- "conditional"：全ての患者について層別にする変数だけを変化させた後、各層毎に統合して生存曲線を描く

methodのデフォルトは"conditional"となっている。

Referenceを"squamous"としてmarginal approachでadjusted survival curveを描いてみる。
Referenceは変数名ではなくデータフレームとして指定。

ggadjustedcurves(fit,data=d, variable="celltype",
                 method="marginal", reference=d[d$celltype=="squamous", ])

図2：Marginal approachを使ってadjusted survival curveを描いた

新規患者に期待される生存曲線

Coxモデルで使用した変数を含んでいる新規データをモデルに代入して、期待される生存曲線を描くことができる。
例えば、「60歳未満の先行治療を受けていない小細胞癌で標準治療を受けた患者」に期待される生存曲線は次のコードで描ける（はず）。

new_patient <- data.frame(trt="standard", age_cat="under60", 
                          celltype="smallcell", prior="N")
ggadjustedcurves(fit, data=new_patient)