高校生のためのデータ分析入門 (18)：曲線を当てはめる

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (17)：複数の説明変数を使った回帰モデル - ねこすたっと

曲線的な関係を当てはめる
線形回帰モデルとは？
おまけ：指数関数を当てはめる
おわりに

曲線的な関係を当てはめる

これまで、回帰モデルでは直線や平面など、曲がっていない関係性を当てはめてきました。今回は、「曲線的な関係性」を当てはめてみましょう。次のような、新興感染症の患者数のデータを例に考えていきます。

説明変数（X）：初めて確認されてから経過した日数
応答変数（Y）：累積感染者数*1

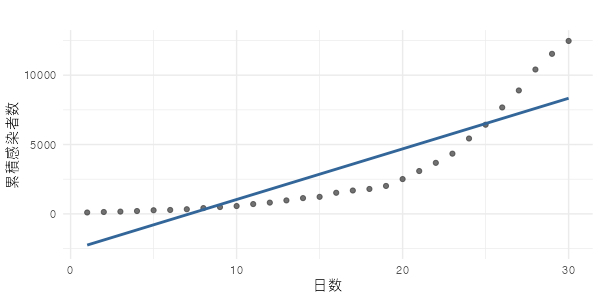
直線を当てはめてみると、下のようになりました。

「単調増加している」という大まかな傾向はつかめていますが、ズレているところも目立ちますね。20日目は実際よりも回帰直線が大きく上を行っていますし、30日目は逆に回帰直線がだいぶ下に来ています。このデータには、直線よりも曲線を当てはめる方がズレが少なくて済みそうです。

曲線を使いたいときは、2次関数が一番お手軽です。 2次関数の一般式は y = ax² + bx + c ですから、期待値のモデル式は次のようになります。

$\begin{aligned} E[Y|X] &= \beta_0 + \beta_1 X + \beta_2 X^2 \end{aligned}$

直線を当てはめたときに比べると、ズレの具合はだいぶ小さくなりましたね！

線形回帰モデルとは？

これまで紹介してきたモデルは、全て「線形回帰モデル（linear regression model）」と呼ばれるものです。どういうモデルのことなのか、まとめてみます*2。

変数の種類

まず、線形回帰モデルは、応答変数が連続変数のときに用いることができるモデルです。なぜなら、誤差が正規分布に従うことを想定しているからです。正規分布は連続変数の分布の代表格でしたね。

一方、説明変数は連続変数でなくても構いません。カテゴリー変数を説明変数としたモデルについては、次回説明します。

変数の個数

応答変数は1つでなければなりません。応答変数が2つあったら、そのYを決める「期待値＋誤差」の式がもう1つ必要になってしまいます。

これに対し、説明変数は（理論的には）いくつあっても構いません（複数の説明変数を含むモデルは前回取り上げましたね）。ただし、サンプル数に比して説明変数の個数が多すぎたり、類似した情報を持った説明変数（例：身長と座高）が含まれていると、推定が上手くいかないことがあります。

期待値が「線形式」で表される

「線形」は英語にするとlinear（リニア、直線）なので、線形回帰モデルは「期待値が直線で表されるモデル」と考えたくなりますが、そういうわけではありません。実際、さっき曲線を当てはめた例を出しました。

線形回帰モデルでは、期待値を決める式に係数βがいくつか含まれていますが、それぞれの係数βについては1次式になっています（つまり、係数同士の積はない）。1次式は直線的な関係を表す式ですから、期待値が係数βの1次式で表されているモデルを「線形回帰モデル」と呼ぶのです。

例えば、次の式で表されるモデルは線形回帰モデルではありません（非線形モデル（non-linear model）といいます）。

例1： $E[Y|X] = \beta_0 e^{\beta_1 X}$
例2： $E[Y|X] = \frac{\beta_0 X}{\beta_1 + X}$

おまけ：指数関数を当てはめる

累積感染者数のモデル化では、2次関数を使うことで残差は小さくなりましたが、逆に問題が出てきてしまいました（わかりますか？）。

累積感染者数というのは、新しく発生した感染者の数を足していきますが、治った人や亡くなった人の数を引くことはありません。つまり、単調増加する数値なのです。応答変数の期待値は単調増加するはずなのに、2次関数は単調増加ではありません。実際、さっき当てはめた曲線も前半のところで減少している部分が出てしまっています。

では、単調増加する曲線を当てはめればいい、ということになります。単調増加する曲線の代表は指数関数です。また、指数関数 y = a^x は常に正なので、累積感染者数の期待値として負の値を返してしまうことがない、というのもイイところです（1次式、2次式では、期待値がマイナスになってしまっている部分がありました）。

そこで、期待値のモデル式を次のようにしました。

$\begin{aligned} E[Y|X] &= c a^X \ \ \ (a>0, c>0) \end{aligned}$

ここで、aはXが増えたときに、Yがどれくらい急峻に増加するかを決めます。 cは、X=0のときのYの期待値、つまりy軸の切片を決めます。

これは先程説明した非線形モデルの例1と同じような式ですね。このままだと線形回帰モデルとして考えることができません。そこで、両辺の対数を取ってみます。

$\begin{aligned} E[\log(Y)|X] &= \log (c a^X) \\ &= \log c + X \log a \end{aligned}$

ここで、 $Y^* = \log(Y)$ で定義される変数Y*を考えます。Yがデータとして収集されていれば、 $Y^*$ もデータとして作ることができますよね。 $Y^*$ のことを「Yを対数変換した変数」などと言ったりします。見やすいように係数も $\log (c) = \beta_0$ , $\log (a) = \beta_1$ として書き直すと、