高校生のためのデータ分析入門 (24)：離散型アウトカムの回帰モデル（後編）

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (23)：離散型アウトカムの回帰モデル（前編） - ねこすたっと

平均値が大きくない個数・回数をモデル化する
小さい非負整数のモデル化
係数はどう解釈したらいいの？
おわりに

平均値が大きくない個数・回数をモデル化する

前回、線形回帰モデルが上手く当てはまらない例として、2値型の応答変数に対してロジスティック回帰モデルを使うことを説明しました。今回は、別の例として、「平均値が大きくない個数・回数」をモデル化してみます。

小さい非負整数のモデル化

例えば、あなたが毎日校内の自販機を見回って、おつり取り忘れをチェックしているとしましょう。頑張って見回ると2日に1件くらいは取り忘れがあるようです。過去1年分のデータを使って、気温と取り忘れ件数の関係を調べたいと思います。

説明変数X：最高気温
応答変数Y：1日の取り忘れ件数

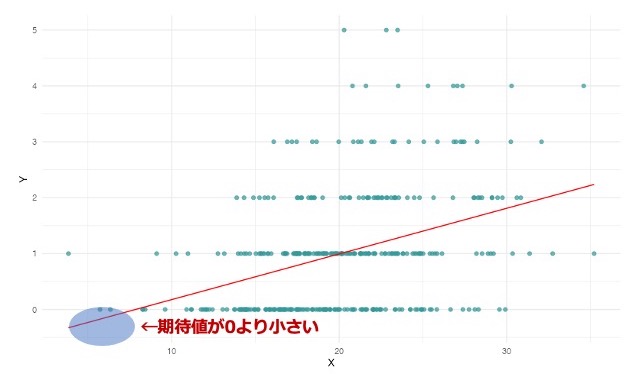
応答変数は0以上の整数（非負整数）ですが、平均が小さいので正規分布を使ったモデル、つまり線形回帰モデルに当てはめるのは難しそうです。

期待値を説明変数の関数で表す

まずは、線形回帰モデルと同じように、期待値を説明変数の関数で表してみます。

$\begin{aligned} E[Y_i|X_i] &= \beta_0 + \beta_1 X_i \end{aligned}$

としたいところですが、2値変数のモデル化と同じく問題が...。

応答変数は取り忘れ件数なので、左辺の期待値は0以上になります。これに対して、右辺 $\beta_0 + \beta_1$ はβやXの値によっては負になることがありえます。負になってしまった値は、平均取り忘れ件数として解釈できません。

対数変換でつなぐ！

期待値が割合を表しているとき、つまり0から1の範囲しか取らないときは、ロジット変換でつなぐことを紹介しました。

necostat.hatenablog.jp

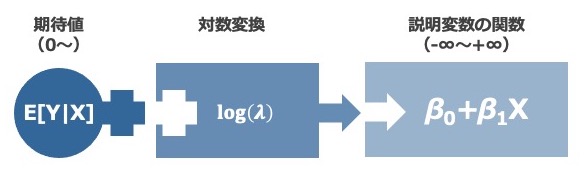
「件数の平均」のように、期待値が正の数しかとらないときは、下のように期待値を対数変換すれば上手くつなげられます。

$\begin{aligned} \log \left( E[Y_i|X_i] \right) &= \beta_0 + \beta_1 X_i \end{aligned}$

対数関数は、単調増加関数で、正の数を真数（logXの中身X）にとり、変換後の範囲は-∞から+∞をカバーします。 $\beta_0 +\beta_1 X$ がどんな値になろうとも、対応する $E[Y|X$ ] は1つに決まります。

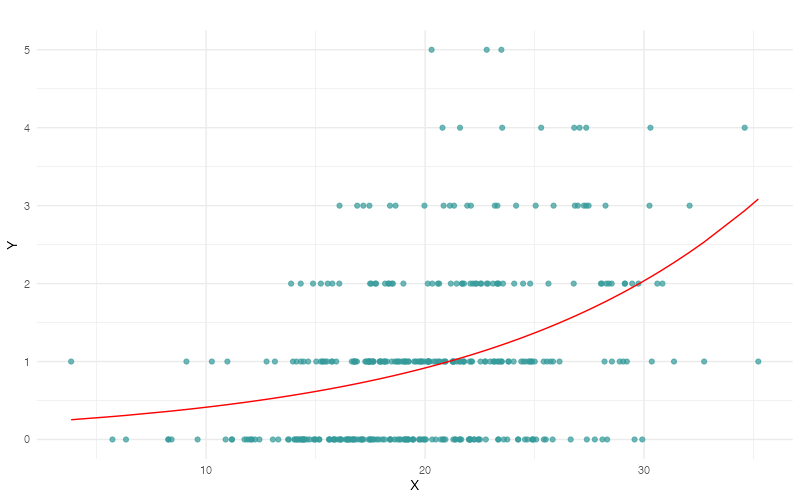
当てはめるとこんな感じ。

期待値と観測値をポアソン分布で結ぶ

期待値が同じでも実際に観察される値は同じとは限りません。例えば、気温から予想される取り忘れ件数が1件だったとしても、実際には0件のこともあれば、（稀ですが）5件もあることもありえます。このギャップを埋めるのが「応答変数はどのような確率分布にしたがうと考えるか」で、ロジスティック回帰モデルでは、2値型の応答変数が二項分布（ベルヌーイ分布）に従うと仮定しました。今回は「平均値の小さい個数・回数」なので「ポアソン分布に従う」と仮定するのが良さそうです。

まとめ：ポアソン回帰

今回の例で想定した以下の式で表されるモデルは、ポアソン回帰モデル（Poisson regression model）と呼ばれます。見やすさのためE[Y|X] = λと書き直しました。

$\begin{aligned} \log \left( \lambda_i \right) &= \beta_0 + \beta_1 X_i \\ Y_i &\sim Poisson(\lambda_i) \end{aligned}$

これを日本語で噛み砕くと、

説明変数 $X_i$ の線形関数として平均件数 $\lambda_i$ が決まる。つまり、それぞれの日は $X_i$ に応じて $\lambda_i$ が与えられる。
説明変数と平均係数を直接はつなげないので、対数変換を介してつなぐ。
応答変数 $Y_i$ は、平均件数 $\lambda_i$ をパラメータとするポアソン分布に従う。

図で表すとこんな感じです。

係数はどう解釈したらいいの？

線形回帰モデルと同様、E[Y|X=x+1]（=λ1）とE[Y|X|x]（=λ0）の差を計算してみます。対数を指数に直してやると、

$\begin{aligned} \lambda_1 &= e^{\beta_0 + \beta_1 (x+1)} \\ \lambda_0 &= e^{\beta_0 + \beta_1 x} \\ \end{aligned}$

指数関数同士の引き算になって、上手く整理できません。

そこで、ロジスティック回帰モデルのときと同じように、期待値の対数で計算してみましょう。

$\begin{aligned} \log \left( \lambda_1 \right) &= \beta_0 + \beta_1 (x+1) \\ \log \left( \lambda_0 \right) &= \beta_0 + \beta_1 x \\ \end{aligned}$

第1式から第2式を引くと、

$\begin{aligned} \log \left( \lambda_1 \right) - \log \left( \lambda_0 \right) &= \beta_1 \end{aligned}$

となります。左辺をlogA-logB=log(A/B)で整理すると、

$\begin{aligned} \log \left( \frac{\lambda_1}{\lambda_0} \right) &= \beta_1 \\ \frac{\lambda_1}{\lambda_0} &= e^{\beta_1} \end{aligned}$

となりました。

ここで、左辺は「X=x+1のときの平均件数」と「X=xのときの平均件数」の比ですので、係数βを指数変換したもの $e^{\beta}$ を使えば、「説明変数が1単位変化したときに、平均件数が何倍になるか」を推定できることになります。

ところで、今回の例の「1日あたりのおつり取り忘れ件数」は、「ある一定期間において観察される数量」ですので、「率」になります（割合と率の違いはこちらを復習！）。この言葉を使えば、 $e^{\beta}$ は「説明変数が1単位変化したときの率比（rate ratio）と解釈できる」と言うことができます。

おわりに

前回と今回で「一般化線形モデル（generalized linear model, GLM）」と呼ばれるモデル（のごく一部）を紹介しました。
GLMは「期待値と説明変数の関数をどのようにつなぐか（リンク関数, link function）」と、「応答変数がどのような確率分布に従うか（分布族, distribution family）」の2つで特徴が表されます。
次回：高校生のためのデータ分析入門 (25)：P値はどうやって計算するの？ - ねこすたっと

ランキング参加中

統計