ねこすたっと

ねこの気持ちと統計について悩む筆者の備忘録的ページ。

高校生のためのデータ分析入門 (19)：カテゴリー変数を説明変数に使う

elementary

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (18)：曲線を当てはめる - ねこすたっと

カテゴリー変数も数字で扱う
- 係数はどう解釈したらいいの？
カテゴリーが3つ以上あるとき
- ダミー変数を使う
おわりに

カテゴリー変数も数字で扱う

以前、変数には量的変数と質的変数があると説明しました。

necostat.hatenablog.jp

質的変数は対象が属するグループを示す変数で、カテゴリー変数（categorical variable）とも言うんでしたね。例えば、性別というカテゴリー変数は、

男, 男, 女, 男, 女, ...
M, M, F, M, F, ...

などのように、変数の取る値が「グループ名を表す文字・記号」を使って表されます。しかし、回帰モデルで扱うためには数式に組み込めないといけませんので、カテゴリー変数も数値として扱う必要があります。

そこで、男=0, 女=1として、

0, 0, 1, 0, 1, …

のようにします。もちろん、男女は逆でも構いません。どの数字がどのグループを意味しているのか明確にしていれば、0,1の代わりに、1,2を使っても構いません。しかし、一般的には0,1を使います。グループを0,1で定義しておけば、変数の平均値が「1が表すカテゴリーの割合」になって便利だからです。

係数はどう解釈したらいいの？

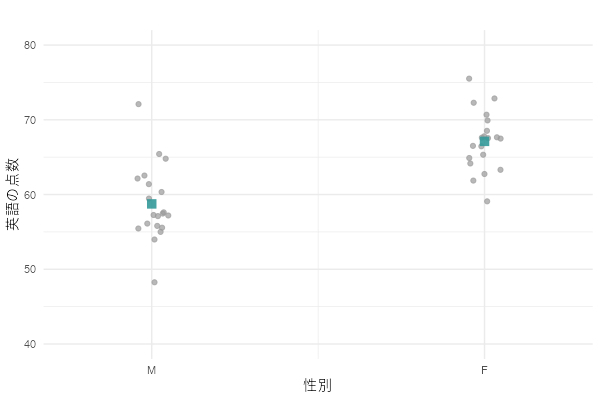
例えば、性別と英語の点数のデータに回帰モデルを当てはめるとします。

説明変数（X）：性別（0=男, 1=女）
応答変数（Y）：英語の点数

データの分布を下に示します。Xは0か1しか取らないので、普通にプロットすると点が重なってよく分からなくなってしまいます。そこで、ランダムに左右にずらして描き込みました*1。ちなみに、緑の四角はそれぞれのグループの平均値です。

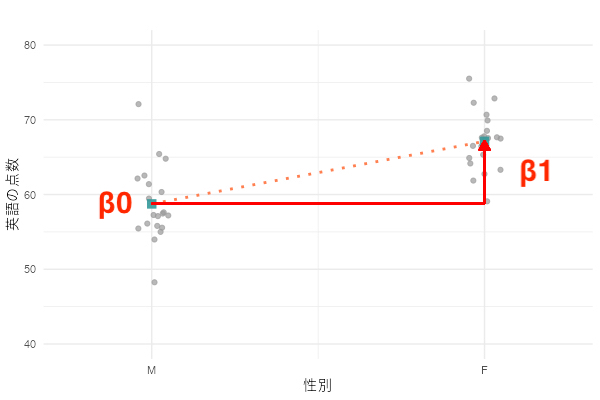
下の式のような線形回帰モデルを当てはめたとしましょう。

$\begin{aligned} E[Y|X] &= \beta_0 + \beta_1 X \end{aligned}$

回帰直線を重ねると、下のようになります。

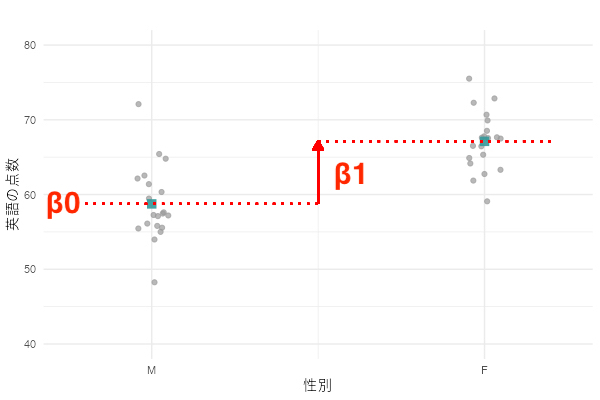
傾き $\beta_1$ は、Xが1単位増えたときのYの期待値の変化量でしたね。ここではXは0か1しか取らないので、「X=0のときに比べて、X=1のときには期待値がどれくらい違うのか」を表している、と解釈します。カテゴリー変数はXが取りうる値が飛び飛びなので、「回帰直線の傾き」というよりも、「期待値の増分（下図）」という方が適切かもしれませんね（見方の違いだけです）。

係数の意味するものを整理すると、

$\beta_0$ ：男子（X=0）の平均値
$\beta_0 + \beta_1$ ：女子（X=1）の平均値
$\beta_1$ ：男子と女子の平均値の差（女子 - 男子）

カテゴリーが3つ以上あるとき

例えば、英語の先生が授業についてアンケートを取ったとしましょう。アンケートでは、授業のわかりやすさを「普通にわかりやすい・とてもわかりやすい・めちゃめちゃわかりやすい」の中から1つ選んで答えてもらいます。

説明変数（X）：アンケートの回答
応答変数（Y）：英語の点数

アンケートの回答はカテゴリー変数ですが、次のように数値を割り振ってみましょうか。

0 = 普通に〜
1 = とても〜
2 = めちゃめちゃ〜

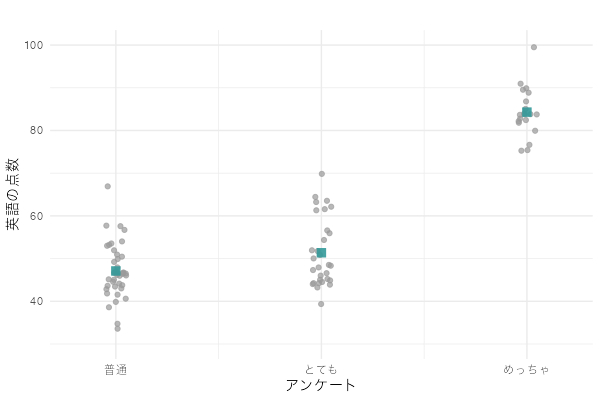
データの分布は下のようになっています。

下の式で表される、さっきと同じモデルを当てはめてみましょう。

$\begin{aligned} E[Y|X] &= \beta_0 + \beta_1 X \end{aligned}$

各グループの平均値は、

「普通に（X=0）」： $\beta_0$
「とても（X=1）」： $\beta_0 + \beta_1$
「めっちゃ（X=2）」： $\beta_0 + 2 \beta_1$

となります。グラフにすると下のとおり。

計算された傾き $\beta_1$ は、Xが1単位増えたときのYの期待値の変化量ですが、これはXが0→1のときも、1→2のときも同じになっています。

でも実際のデータは、一定の傾きではないようです。0→1よりも1→2の方が、英語の点数はグッと高くなっていますね。先程のモデル式では、どう頑張っても0→1と1→2で増分が同じになってしまい、増分の違いは表現できません。さらに、回帰直線はそれぞれのグループの平均値を通っていません。

「2次関数を当てはめる」というのも1つの作戦かもしれませんが、0→1と1→2で別々の増分を設定したモデルを使う作戦が一般的です。

ダミー変数を使う

そこで次のように、「それぞれのカテゴリーに当てはまるかどうか」を示した2値変数を導入します。

$X_1$ ：「とても〜」なら1、それ以外は0を取る
$X_2$ ：「めちゃめちゃ〜」なら1、それ以外は0を取る

$X_1$ も $X_2$ も0であれば、「普通に〜」を表すことになるので、 $X_0$ を導入する必要はありません。

このように、k個のカテゴリーを持つ変数は (k-1)個の2値変数の組み合わせで表すことができます。このときに用いる2値変数をダミー変数（dummy variable）と呼びます。

ダミー変数に変換したデータに対して、下のようなモデルを当てはめます。元のカテゴリー変数Xではなく、2つのダミー変数を説明変数にしたモデルです。

$\begin{aligned} E[Y|X] &= \beta_0 + \beta_1 X_1 + \beta_2 X_2 \end{aligned}$

このモデルのもとで、それぞれのカテゴリーの平均点は、次のようになります。

「普通に」： $\beta_0$
「とても」： $\beta_0 + \beta_1$
「めっちゃ」： $\beta_0 + \beta_2$

グラフにすると下のとおり。

こうすれば、X=0→1の増分は $\beta_1$ 、X=0→2の増分は $\beta_2$ になるので、0→1と0→2で別々の増分を設定することができました。

例の「普通に〜」のように、全てのダミー変数=0で表されるカテゴリーは、他のカテゴリーの比較対照になります。このように比較の基準となるカテゴリーを参照カテゴリー（reference category）と呼びます。

おわりに

これで線形回帰モデルについて基本的なことは押さえました。
連続型ではない応答変数に用いる回帰モデルについては、いずれ学んでいきましょう。
次回：高校生のためのデータ分析入門 (20)：期待値と分散・共分散の計算シャワー - ねこすたっと

ランキング参加中

*1:jitteringと言います