ねこすたっと

ねこの気持ちと統計について悩む筆者の備忘録的ページ。

分散分析（ANOVA）：固定効果と変量効果

maths/theory clustered/repeated matching/paired neco

分散分析（Analysis of Variance, ANOVA）を学ぶ目的でKutner先生のApplied Linear Statistical Models（5th edition）を拾い読みし始めました。 前回は二元配置分散分析で分散分析表を作るところまで確認しました。。

necostat.hatenablog.jp

今回は要因の効果をどのように捉えるかについて、"Chapter 25： Random and Mixed Effects Models" を拾い読みします。

基本的な実験デザイン

完全無作為法

最も標準的でシンプルな実験デザインは、実験単位（exprimental unit）をそれぞれの治療群に無作為に割り付ける方法です。 これを完全無作為化法（completely randomized design, CRD）と呼びます。

いま治療a1と治療a2を比較することを想定しましょう。対象者は観察可能な属性（ここでは性別としておきます）によって、治療の効きやすさが異なるとします。

対象者を無作為に割り付けて比較すれば、観察された差は治療の効果の差と考えることができるはずですが、下の図のように、たまたま性別の偏りが生じ、適切に比較することができなくなることがあります。

乱塊法

そこで、ランダム割り付けをする前に、対象者を性別で分けておき、それぞれの性別においてランダム割り付けを行います。こうすれば治療群間で性別の偏りが生じません。 似たもの同士で集められた塊をブロック（block）と呼びます。

このように、対象を似たもの同士集めてブロックとしてから、そのブロックごとに治療をランダムに割り付けるデザインを乱塊法（randomized blocked design, RBD）と言います。

ブロック化に用いられる変数をブロック因子あるいはブロック変数（blocking factor/variable）と言います。ブロック因子に使われるものとしては、(1) 実験単位の特性（年齢、性別、教育など）や、(2) 実験のセッティング（評価者、評価時期、使用機器など）があります。同一個人に対して反復して実験を行うデザイン（repeated measurement design）は、個人をブロック因子としたブロック化の特殊な状況です。

固定効果と変量効果

固定効果（fixed effect）と変量効果（random effect）については以前、マルチレベルモデルを勉強したときに少しだけ触れました。

necostat.hatenablog.jp

ある要因の効果を固定効果と考えるか、それとも変量効果と考えるかは、その要因の効果に興味があるかどうかで判断することが多いようです。

ブロックが評価者や被験者個人の場合は、その個人ごとに効果がどのように違うかに興味がないことがほとんどなので、変量効果として扱うことが多いようです。

一方、ブロックが特定のカテゴリー（例：年齢、収入、処理順序など）によって与えられたものならば固定効果と考えることが多いようです。

「効果が固定されていると考えるか、それともランダム変数と考えるか」という説明をきいてもそんなにスッキリしなかったんですが、モデルの仮定と検証する仮説にもとづいた説明は分かりやすかったです。

Random Cell Means Model*1

前々回の記事で扱ったモデルでは、各群の真の平均値はそれぞれある値に固定されていると考えていました。ここで扱うrandom cell means modelは、各群の真の平均がランダム変数として固定されていないモデルで、数式で表すと下のようになります。

\begin{aligned} Y_{ik} &= \mu_i + \varepsilon_{ik} \\ \mu_i &\sim Normal(\mu_., \sigma_{\mu} ^2) \\ \varepsilon_{ik} &\sim Normal(0, \sigma ^2) \\ \mu_i &\perp \varepsilon_{ik} \end{aligned}

ここで \mu_. は集団全体の真の平均で、各群の平均 \mu_i は \mu_. を中心とした正規分布に従っていて、その分散は \sigma_{\mu} ^2 です。また、 \varepsilon_{ik} は群内誤差を表していて、 \mu_i とは互いに独立と仮定されています。

群内相関

\mu_i と \varepsilon_{ik} が互いに独立なので、観測値 Y_{ik} = \mu_i + \varepsilon_{ik} の分散は、

\begin{aligned} Var\{Y_{ik}\} &= Var\{\mu_i\} + Var\{\varepsilon_{ik}\} + Cov\{\mu_i, \varepsilon_{ik}\} \\ &= Var\{\mu_i\} + Var\{\varepsilon_{ik}\} \\ &= \sigma_{\mu}^2 + \sigma^2 \end{aligned}

となります。Yの分散が群間誤差の分散 \sigma_{\mu}^2 と群内誤差の分散 \sigma^2 から構成されていることが分かります。

固定効果モデルでは全ての観測値 Y_{ik} は互いに独立ですが、変量効果モデルでは異なる群に属する観測値の間でのみ独立であることが仮定されます。

\begin{aligned} Cov \{Y_{ik}, Y_{ik'}\} &= Cov \{\mu_i+\varepsilon_{ik}, \mu_i+\varepsilon_{ik'} \} \\ &= Cov\{\mu_i, \mu_i \} + Cov\{\mu_i, \varepsilon_{ik'} \} + Cov\{\varepsilon_{ik},\mu_i \} + Cov\{\varepsilon_{ik},\varepsilon_{ik'} \} \\ &= Var\{\mu_i \} \\ &= \sigma_{\mu}^2 \\ Cov \{Y_{ik}, Y_{i'k'}\} &= 0 \end{aligned}

上記のように同じ群に属する観測値間の共分散は群間誤差の分散 \sigma_{\mu}^2 になります。同じ群に属するYの相関係数は、

\begin{aligned} Corr \{Y_{ik}, Y_{ik'}\} &= \frac{Cov \{Y_{ik}, Y_{ik'}\}}{SD\{Y_{ik}\} SD\{Y_{ik'}\}} \\ &= \frac{\sigma_{\mu}^2}{\sigma_{\mu}^2+\sigma^2} \end{aligned}

となり、これを級内相関係数（intraclass correlation coefficient, ICC）と言います。

検定する仮説

固定効果ANOVAモデルにおける帰無仮説は「全ての群で群平均が等しい」でした。

\begin{aligned} H_0: &\ \mu_1 = \mu_2 = ... = \mu_a \\ H_A: &\ not \ H_0 \end{aligned}

これに対し、変量効果ANOVAモデルにおける帰無仮説は「群平均の分散が0である」です。 群平均の分散が0であるということ、群平均が全て等しいということを意味しています。

\begin{aligned} H_0: &\ \sigma_{\mu} = 0 \\ H_A: &\ \sigma_{\mu} \neq 0 \end{aligned}

分散分析表

要因が2つ以上の場合、

  • 固定効果ANOVAモデル（Fixed ANOVA model）：
    要因全てについて固定効果と考えるモデル
  • 変量効果ANOVAモデル（Random ANOVA model）：
    要因全てについて変量効果と考えるモデル
  • 混合効果ANOVAモデル（Mixed ANOVA model）：
    固定効果と変量効果の両方を含むモデル

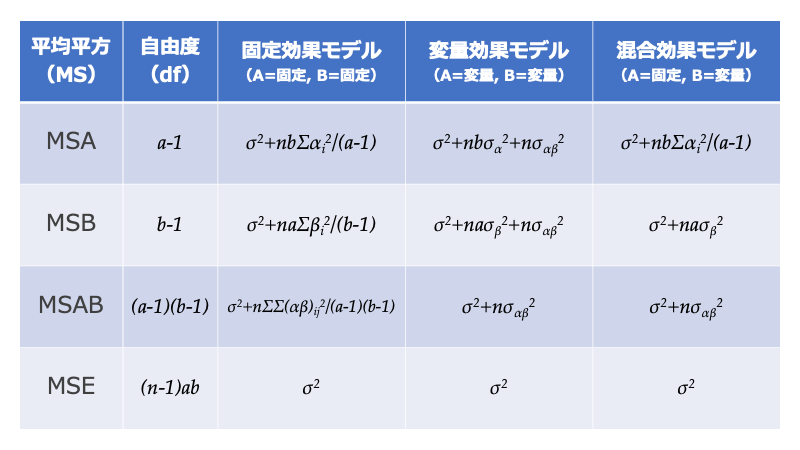
が考えられます。それぞれのモデルにおいて平均平方（MS）が何を推定しているかを表にまとめました（MSについては前回の記事を参照）。

仮説を検定するときは、次のように検定統計量（F統計量）を決めます。

  • 帰無仮説が正しければ、同じ値になることが期待される
  • 対立仮説が正しければ、分子が分母よりも大きな値を取ることが期待される

まとめると下の表のようになります。

おわりに

  • 実験デザインはまだまだ学ぶことがありそうですが、自分はあまり使う機会がなさそうです。
  • これで一旦ANOVAから離れたいと思います。
  • ガツガツ食べて、吐いて、すっきりしてまたガツガツ食べて...（ネコの話です）

ランキング参加中
統計

Applied Linear Statistical Models 5ed (Pb 2013)

Applied Linear Statistical Models 5ed (Pb 2013)

Amazon

*1:ランダムセル平均モデルと書くと平均の部分以外訳せていないのでそのまま英語にしました