ランドマーク解析を使ってimmortal time biasに対処する（dynpredパッケージ）[R]

Immortal time biasとは
ランドマーク（LM）解析とは
dynpredパッケージを使ってシンプルなLM解析を行う
cutLM( )を使わない場合
おわりに
参考資料

Immortal time biasとは

興味ある要因・介入の状態が観察開始後に決まる状況では、要因・介入が発生するまで生存していなければならない。「死んではいけない時間」により生じるバイアスということで、immortal time bias（別名：guarantee-time bias）と呼ばれる。

例えば、移植治療を受けた人と受けなかった人を比較して、介入の効果を見たいとき、診断されて早々に亡くなってしまった人は移植治療群に割り付けられることはないので、介入を受けた方が生存期間が長くなりうる。

Immortal time biasに対処する方法としては、

ランドマーク法を使った解析
時間依存性変数を使った解析

があって、この記事ではRを使って前者を実装する方法を確認してみる。

ランドマーク（LM）解析とは

要因・介入の状態が観察期間の長さに依存してしまうことがimmortal time biasの原因。そこで、臨床的観点から妥当なLM時点（landmark time-point）を設定して、以下の要領でat risk集団と要因・介入の状態を判定する。

LM時点でイベントを発生していない人がat risk集団として解析対象となる
LM時点前に要因・介入が発生した場合に「要因・介入あり」と判定する
LM時点後に要因・介入が発生しても「要因・介入なし」と判定する

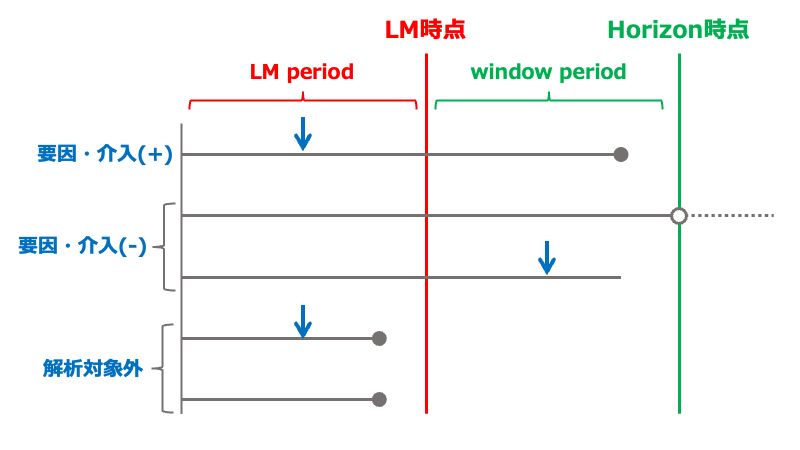
LM時点をスライドさせたり、それらを統合して解析するときには、強制的に打ち切りとする時点（horizon）が設定される。
これによって、LM時点まで生存している条件下で、LMからhorizonまでの期間（window）で予測される生存確率を推定でき、「起算日から何年生存していれば、その後どれくらいの生存が見込めるか」といったような、経過の進行に合わせた予測（動的予測, dynamic prediction）が可能。

dynpredパッケージを使ってシンプルなLM解析を行う

シンプルなLM解析は、まず臨床的に妥当なLM時点を設定してから、個々の患者がLM時点でat riskなのか、そして要因・介入の状態（あり・なし）を判定した変数を作成して、通常どおり生存時間解析を行えば良い。データセットの作成は、if_else( )など基本的な関数を使ってできるけど、後々のことを考えてcutLM( )を使ってみる。

必要なパッケージの読み込みと模擬データ作成

dynpredパッケージを読み込むとsurvivalパッケージも自動で読み込まれる。 Kaplan-Meier生存曲線を描くためにjskmパッケージも入れておく。

necostat.hatenablog.jp

library(dynpred)
library(tidyverse)
library(jskm)

サンプルデータは以下のコードで作成。

set.seed(123)
n = 100
id <- 1:n
age <- runif(n=n, min=50, max=80)
survtime <- round(rweibull(n=n, shape=2, scale=500))
survstat <- rbinom(n=n, size=1, prob=0.6)
trttime <- round(rweibull(n=n, shape=2, scale=500))

age：年齢（時間非依存性変数として作るが解析には使う予定なし）。
survtime：生存時間または打ち切りまでの観察時間（単位はdaysのつもり）
survstat：死亡（=1）または打ち切り（=0）。今回は60%で死亡が観察されていることを想定。
trttime：治療開始までの時間

ageは一様分布から、survtimeとtrttimeはWeibull分布から作成した。

変数をtibble( )*1でデータフレームにする。

d <- tibble(id, age, survtime, survstat, trttime)

ちなみにこの段階での中身は以下のとおり。

> d
# A tibble: 100 × 5
      id   age survtime survstat trttime
   <int> <dbl>    <dbl>    <int>   <dbl>
 1     1  58.6      357        1     246
 2     2  73.6      524        0    1080
 3     3  62.3      423        0     250
 4     4  76.5      108        1     281
 5     5  78.2      427        1     340
 6     6  51.4      170        0     428
 7     7  65.8      150        1     681
 8     8  76.8      352        1    1096
 9     9  66.5      472        1     445
10    10  63.7      692        1     421
# … with 90 more rows

ここで、trttimeがsurvtimeより大きい場合は生存期間中に治療が開始されないことをもとにして、治療状態（trtstat）を定義する（ここでimmortal time biasが発生している）。また、治療が行われない場合はtrttimeをsurvtimeと同じにしておく。

data_orig <- d %>%
  mutate(trtstat = if_else(trttime<survtime, 1, 0),
         trttime = if_else(trttime>=survtime, survtime, trttime))

> data_orig
# A tibble: 100 × 6
      id   age survtime survstat trttime trtstat
   <int> <dbl>    <dbl>    <int>   <dbl>   <dbl>
 1     1  58.6      357        1     246       1
 2     2  73.6      524        0     524       0
 3     3  62.3      423        0     250       1
 4     4  76.5      108        1     108       0
 5     5  78.2      427        1     340       1
 6     6  51.4      170        0     170       0
 7     7  65.8      150        1     150       0
 8     8  76.8      352        1     352       0
 9     9  66.5      472        1     445       1
10    10  63.7      692        1     421       1
# … with 90 more rows

治療開始時間が生存時間より長かった人のデータが適切に修正されていることを確認。

元データを通常どおり解析する

Kaplan-Meier生存曲線とLogrank検定にもとづくP値は以下のとおり。

survfit(Surv(survtime, survstat) ~ trtstat, data = data_orig) %>%
  jskm(pval = TRUE)

治療を行った方が生存時間が長くなっているが、データ生成過程を考えれば当然のこと。

cutLM( )を使ってランドマーク解析を行う

cutLM( )を使ってランドマーク解析用のデータセットを作成する。ここではLM時点を300として、800（LM + horizontal）で強制打ち切りとした。

指定する主な引数は以下のとおり。

data：元データ
outcome：アウトカム発生時間（time）と発生状況（status）を表す変数名をリスト形式で指定。
LM：LM時点。ここでは300日とした。
horizontal：強制打ち切りとする時点。ここでは800日とした。
cov：アウトカム以外の共変量を示す変数名。時間非依存性はfixed=で、時間依存性はvarying=で指定。
rtime：時間依存性変数の観察時点を示す変数
format：元データが横長データ（="wide"）か縦長データ（="long"）かを示す引数（のはずだが、横長データと指定すると治療状態が全て1になってしまう...）
id：患者識別変数

cutLM( )だけで処理を止めると、治療状態が1とNAになってしまうので、NAを0とするような処理を追加している。

LM <- 300
window <- 500
data_LM <- cutLM(data = data_orig,
                 outcome = list(time="survtime", status="survstat"),
                 LM = LM,
                 horizon = LM + window,
                 cov = list(fixed = "age", varying="trtstat"),
                 rtime = "trttime",
                 id = "id",
                 format = "long") %>%
  mutate(trtstat = case_when(trtstat == 1 ~ 1,
                             trtstat == 0 ~ 0,
                             is.na(trtstat) ~ 0))

> data_LM
# A tibble: 74 × 7
      id survtime survstat   age trtstat trttime    LM
   <int>    <dbl>    <dbl> <dbl>   <dbl>   <dbl> <dbl>
 1     1      357        1  58.6       1     246   300
 2     2      524        0  73.6       0      NA   300
 3     3      423        0  62.3       1     250   300
 4     5      427        1  78.2       0      NA   300
 5     8      352        1  76.8       0      NA   300
 6     9      472        1  66.5       0      NA   300
 7    10      692        1  63.7       0      NA   300
 8    12      548        1  63.6       0      NA   300
 9    13      800        0  70.3       1     291   300
10    16      698        0  77.0       1     234   300
# … with 64 more rows

元のdata_origデータと見比べて、以下のことが確認できた。

症例4はLM時点（=300日）前に死亡しているので除外されている
症例9は445日目に治療を受けているが、これはLM時点後なのでtrtstat=0となっている
症例13は837日目に死亡発生しているが、LMデータセットでは800日で強制打ち切りに変換されている

このデータセットで先程と同様の解析をすると、

survfit(Surv(survtime, survstat) ~ trtstat, data = data_LM) %>%
  jskm(pval = TRUE)

300日前に死亡している人は含まれないので、300日時点までは生存確率は1のまま。最後は800日目で打ち切りとなっている。LM解析をすると治療有無による差は消失している。

cutLM( )を使わない場合

LM時点やhorizon時点と同時点の扱いがどうなるかを確認したところ、

死亡発生時点がLM時点と同じときは「解析対象外」の扱い
治療開始時点がLM時点と同じときは「治療なし」の扱い
死亡発生時点がhorizon時点と同じときは死亡発生扱い（horizon時点までは観察されていることになる）

となっている模様。なのでコードにすると下のとおり。

data_LM2 <- data_orig %>%
  filter(survtime > LM) %>%
  mutate(trtstat = if_else(trttime < LM, 1, 0))
data_LM2$survstat[data_LM2$survtime > LM+window] <- 0
data_LM2$survtime[data_LM2$survtime > LM+window] <- LM+window

要約値はdata_LMと一致していたので多分大丈夫だろう（もう少し綺麗なコードにしたかった...）。

おわりに

解析そのものよりも特定のLM時点を選ぶ方が難しそう。なので「LMを順番に変化させていったときに、要因・介入の効果（=ハザード比）がどのように変化していくか」を示す方がよさそう。
上記のことを解決すべく、次回はスーパーランドマークモデルを使った解析をやってみたい。
第6シーズンは諦めて、不定期更新で細々と頑張ります。