ねこすたっと

ねこの気持ちと統計について悩む筆者の備忘録的ページ。

高校生のためのデータ分析入門 (5)：グラフにするのは超大事！（後編）

elementary presentation reporting

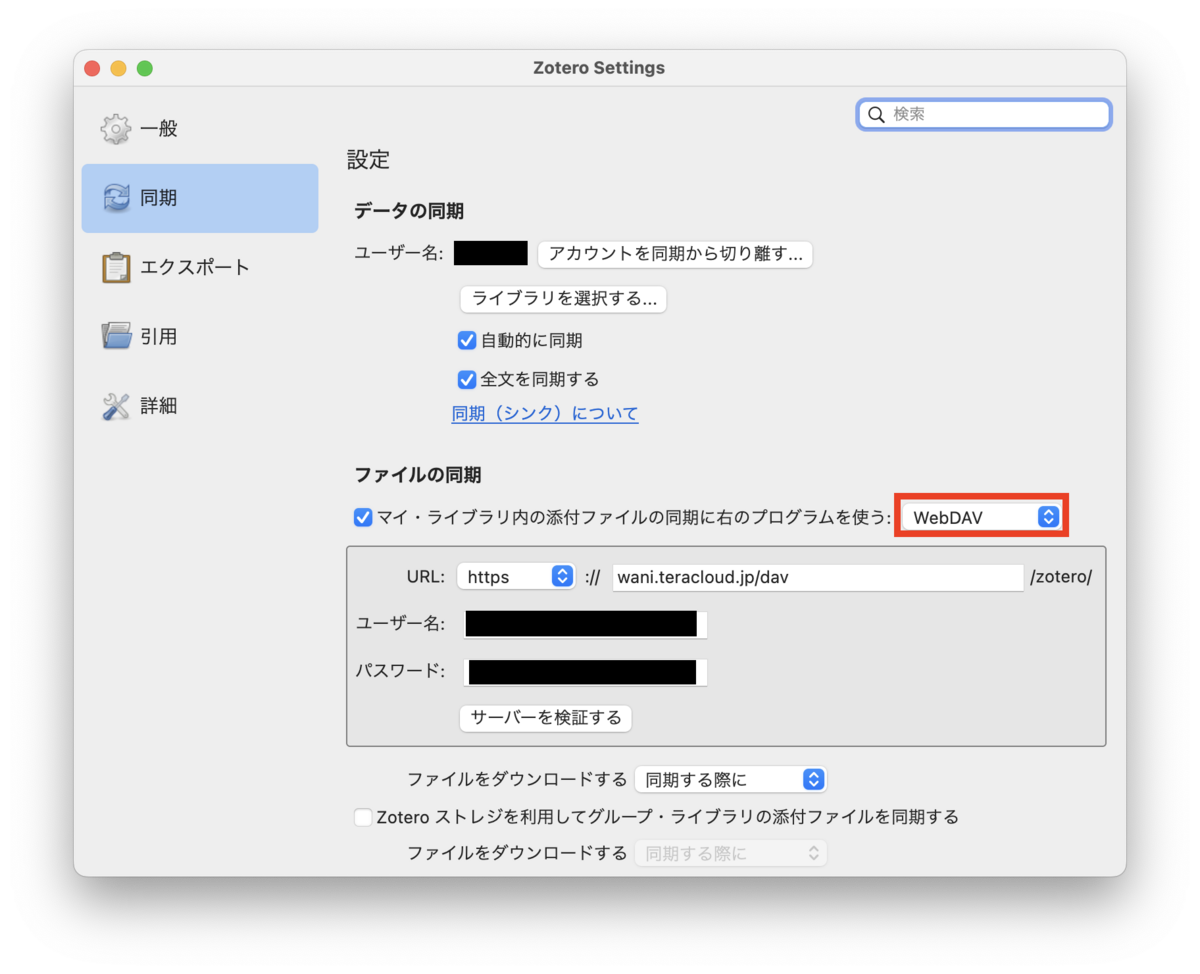
数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回のおさらい

前編では、グラフを

  • 軸をどうやって表すか（縦軸・横軸・色など）
  • 軸に何を割り当てるか

という観点で整理しようという抽象的な話をしました。

necostat.hatenablog.jp

今日は具体例を見ていきましょう。

変数が1つのとき

1つの質的変数を示す

あるクラスの血液型の分布を例にして考えてみます。 1つ目の軸には変数が取る値を割り当てます。質的変数は、2つ目の軸を使って個数・割合をで示さないといけないんでしたね。整理すると次のように書けます。

  • 1つ目の軸：A型、B型、O型、AB型
  • 2つ目の軸：それぞれの血液型に属する人数（または全体に占める割合）

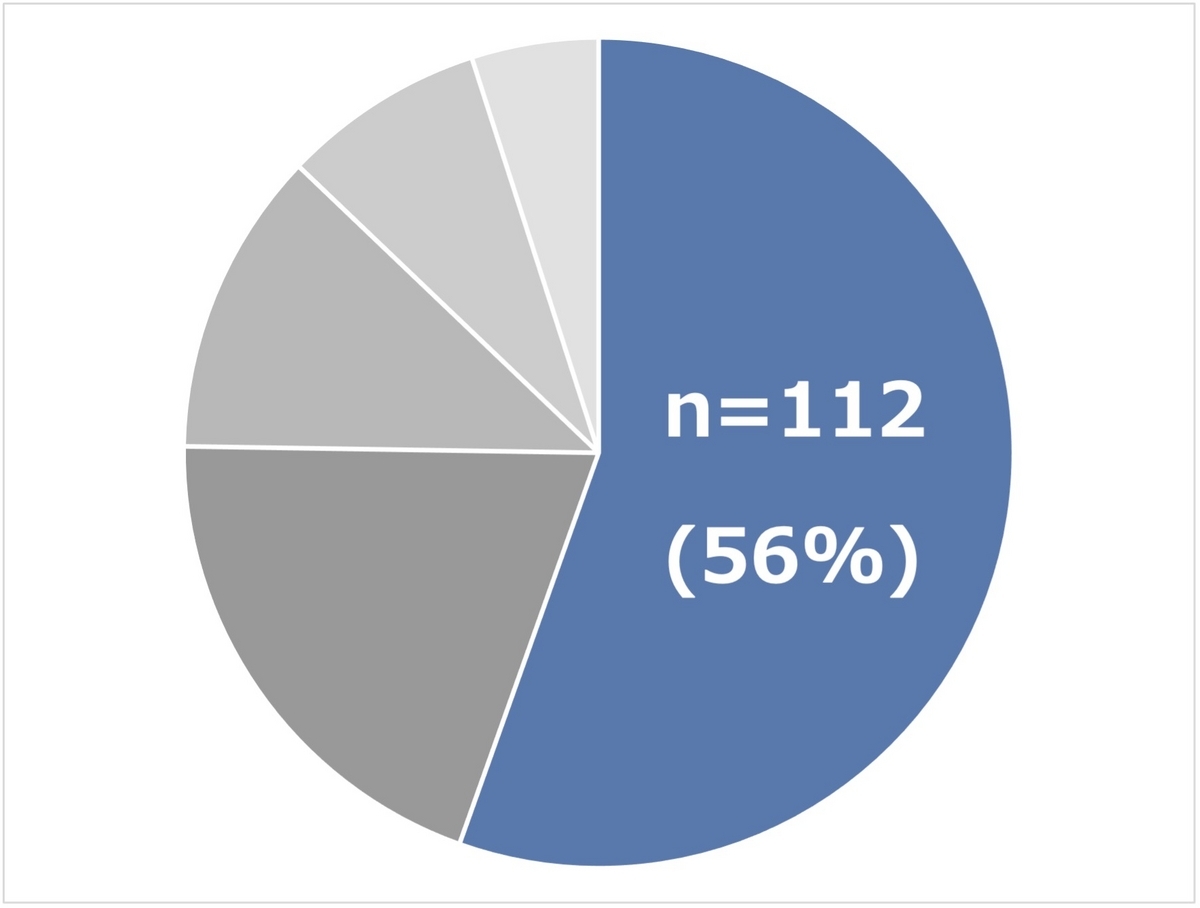
カテゴリー毎の個数や割合を、高さで表せば、棒グラフ（bar chart）、 長さで表せば水平棒グラフ、角度（つまり弧の長さ）で表せば、円グラフ（pie chart）になります。 これらは表したいものは同じで、見せ方が違うだけなんです。

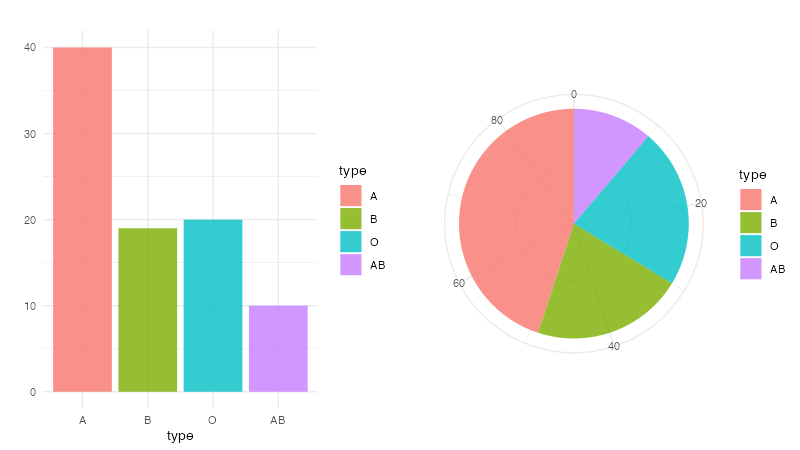
では、棒グラフと円グラフ、どちらを使う方が良いんでしょうか？

円グラフの方が人気がありますが、原則として棒グラフを使います。円グラフだと微妙な大小関係が読み取りにくいからです。先程のグラフで、B型とO型のどちらが多いか、円グラフから読み取れますか？

例外としては、「あるカテゴリーがこんなに占めてますよ！」みたいなことをアピールしたいときは円グラフの方がインパクトが出るかもしれませんね。

1つの量的変数を示す

量的変数はそのまま1つ目の軸で示すことができます。それぞれの値をプロット*1するか、それで見にくくなるなら要約値をプロットすればいいのです。

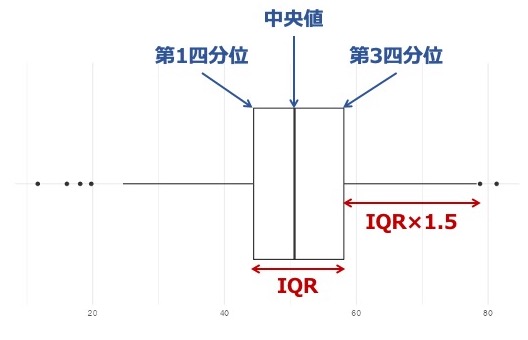
複数の要約値をまとめて示す方法として、箱ひげ図（box-whisker plot）という方法があります。 これは、中央値・四分位範囲（IQR）と外れ値の様子を分かりやすく示すことができるグラフです。

  • 箱の中央線 = 中央値
  • 箱の両端 = IQRの両端（第1四分位数、第3四分位数）
  • 箱の両端から伸びるヒゲ = 第1四分位数（あるいは第3四分位数）の外にある点で、IQR×1.5以内にある点のうち、最も箱から遠いところを示す。
  • 点 = 上記のヒゲよりも外側にある点

上記の加えて、平均値を示すこともできます。

もう1つの量的変数の示し方は、カテゴリー化する方法です。 例えば、年齢をそのまま使えば量的変数ですが、10代、20代、30代というカテゴリーで区別すれば、質的変数として扱うことになりますので、カテゴリー毎の人数を帯状にすれば下のようになります。

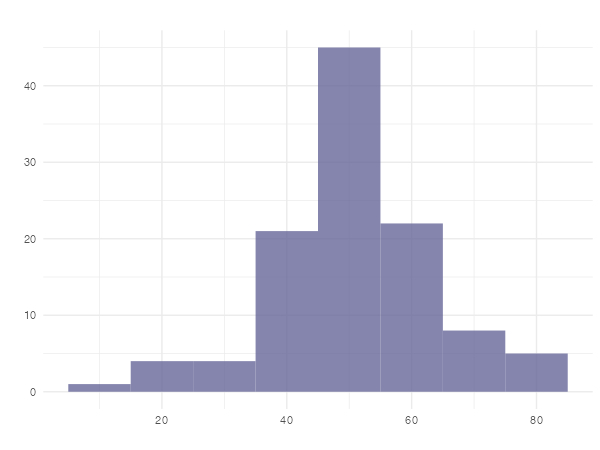
ヒストグラム（histogram）は棒グラフと似ていますが、隙間がない点が違います。量的変数をカテゴリー化すると、隣り合うカテゴリーは隙間なく連続しているからです。区間の右端が「以下」なのか「未満」なのか、統一して決めておかなければいけません。

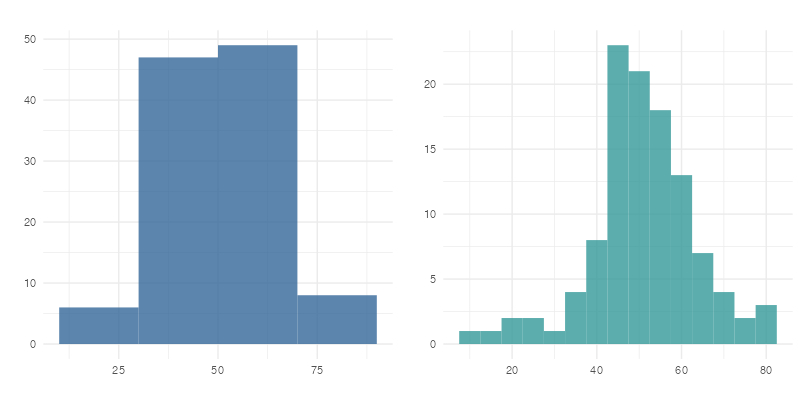
また、ヒストグラムでは区間の決め方によってグラフの印象が大きく変わることがあります。下の図では、同じデータを20歳刻み（左）と5歳刻み（右）で描きました。

ヒストグラムの親戚に密度プロット（density plot）というグラフがあります。これはヒストグラムの区間を限りなく小さくしながら、ヒストグラムのデコボコが滑らかな曲線になるようにしていったグラフです。

変数が2つのとき

2つの量的変数を示す

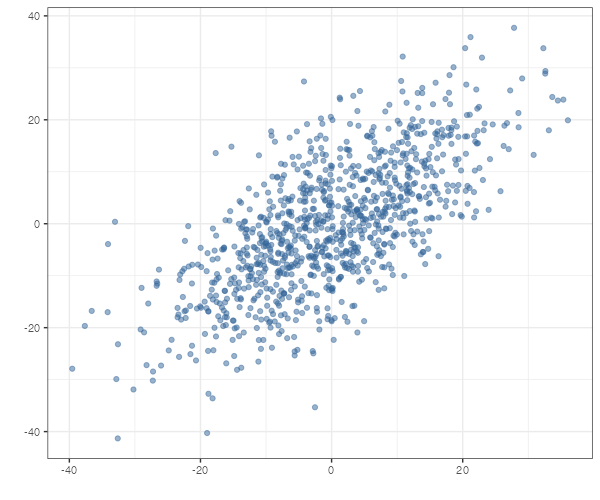
2つの量的変数をx軸、y軸にして点(x,y)を座標平面にプロットするグラフを散布図（scatter plot）といいます。

1つしか軸がないときに値をプロットすると重なって見にくくなってしまいましたが、2つ軸があれば大丈夫ですね。もし重なりが多くて見にくくなるときは、点を半透明にしてやると多少見やすくなります。

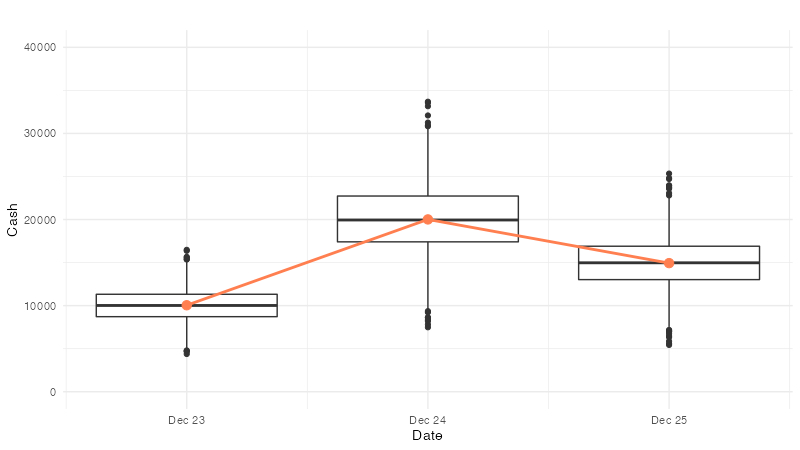
それでも見にくいときは、一方を要約値にしてやればいいです。例えば、USJに遊びに来た人について、横軸に来場日、縦軸に来場者が持ってきた現金の金額をプロットすることを想像してみましょう。おそらく来場者が多すぎて、普通にプロットすると重なってよく分からなくなりますね。そこで、要約値をプロットしてやれば見やすくなります。下のグラフでは箱ひげ図と平均値（赤）を重ねて描きました。

この例のように、時間的な変化を示す場合に限っては、折れ線でつないでもいいです。

量的変数と質的変数が1つずつ

質的変数の水準別に量的変数の分布を示します。 例えば、生徒の血液型と数学の点数を表すグラフを考えましょう。

1つ目の軸に血液型を割り当てて、2つ目の軸に数学の点数を割り当てます。人数が少なければあまり重なりも気にならずにプロットできますね。人数が多ければ箱ヒゲ図で要約値をプロットするか、ヒストグラム（あるいは密度プロット）で示すとスッキリします。

下のグラフは、バイオリンプロット（violin plot）と呼ばれるもので、密度プロットを両側対称にしたものです。

2つの質的変数を示す

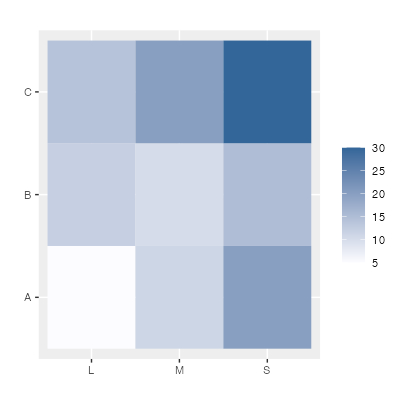
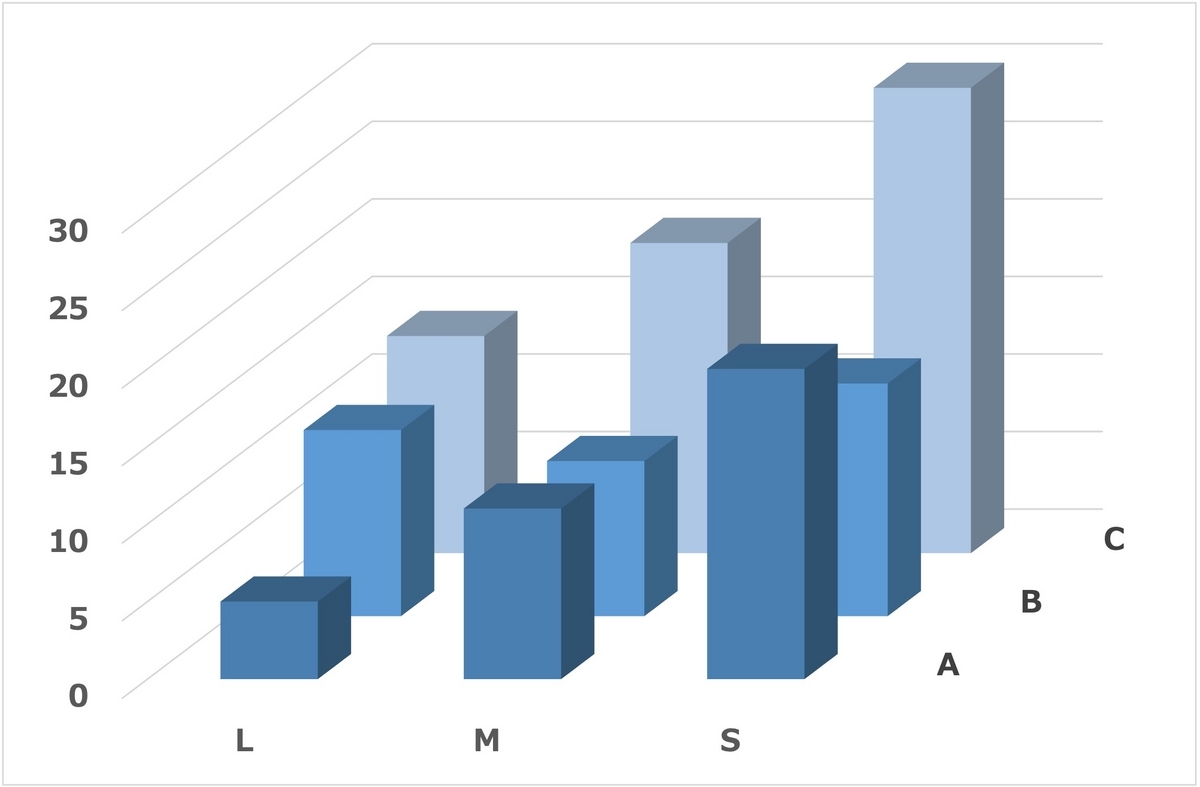
2つの質的変数を2つの軸で表すことはできません。質的変数はプロットの重なりが避けられないからです。3つ目の軸を高さにすることは極力避ける、と説明しましたね。色などを使って表せないか考えてみましょう（下は再掲です）。

おわりに

ランキング参加中
統計

*1:点を打つこと

高校生のためのデータ分析入門 (4)：グラフにするのは超大事！（前編）

elementary presentation reporting

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (3)：変数の分布を数値で示す - ねこすたっと

適切なグラフを選ぶポイント

変数の分布を数値で要約すると、分布の様子に関して多くの情報が失われてしまうことは、前に説明したとおりです。なので、データ分析で扱う変数は要約値だけを見るのではなく、必ずグラフを描いて確認するようにしましょう。

今は高校生でもエクセルを使う機会がありますし、おすすめのグラフを提案してくれたりします。頼るのはいいですが、どのようなデータにはどのようなグラフが適しているのか、一度は確認しておきましょう。

グラフの選び方を2つのポイントから整理します。

軸（要素）は3つまで

グラフはデータが持っている変数や要約値を、平面上に描いて見せるものです。平面は縦と横の2方向の軸があるので、グラフには少なくとも2つの要素を盛り込むことができます。

ときどき下のような、高さを軸に追加した3Dグラフを見たことがあるかもしれませんね。3Dグラフは一見カッコ良さそうに見えますが、極力避けましょう*1。影になっているところが分からなかったり、大小関係が伝わらなかったりするからです。下のグラフでM-AとM-Bとどちらが大きいか、すぐに分かりますか？

3Dグラフを避けるには、3つ目の要素*2を「点・線・面」を変えることで表現できないかを考えます。

  • 点：プロットする記号の種類（⚪︎, +, ▲など）、色、大きさ
  • 線：種類（実線、点線など）、色
  • 面：塗り方のパターン、色

例えば、3つ目の要素（=カテゴリーに属する個数）を色で表すと、下のようになります。

「3つ目の要素は色で区別して、4つ目の要素は塗り方で区別して、...」ということは理論上は可能ですが、おそらくかなり判別しにくいグラフになるでしょう。なので、要素は3つまでに留めておくことをお勧めします。

何を軸（要素）に割り当てるか

まず1つ目の軸に、興味のある変数がとりうる値を割り当てます。下の図のように、質的変数であれば各水準を軸に沿って並べます。量的変数であれば、数直線のように目盛りを振ります。

最も簡単なグラフは、その変数が実際に取っている値をこの軸上にプロットしたものです。しかし、質的変数では点が重なってしまい、いくつあるのか分からなくなってしまうでしょう。そこで質的変数の場合は、2つ目の軸を使って個数・割合という要約値を示すことになります。

量的変数でも観察数が増えてくると判別が難しくなりますが、要約値（平均など）を示すだけであれば十分読み取ることができるでしょう。

2つ目以降の軸（要素）にも同じように、変数の取りうる値や、要約値を割り当てていきます。2つ目に別の質的変数を割り当てたときは、個数を示すために3つ目の軸が必要になります。

おわりに

  • 少し抽象的な説明で難しかったかもしれません。後編では具体例を出します。
  • 軸をどうやって表すか（縦軸・横軸・色など）と、軸に割り当てる項目を別々に整理することで、たくさんありそうなグラフを整理できるよ、という話でした。
  • グラフを描くときは、文字の大きさ、軸の名前、凡例など細かいところにも気を配らないといけません。そこらへんは手を抜いてます。
  • 次回：高校生のためのデータ分析入門 (5)：グラフにするのは超大事！（後編） - ねこすたっと

ランキング参加中
統計

*1:ホログラムが一般的になった世界ならまた話は違うかもしれません

*2:「3つ目の軸」と言うと誤解を招きそうなので「要素」と言い換えました

高校生のためのデータ分析入門 (3)：変数の分布を数値で示す

elementary presentation reporting terminology

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (2)：変数ってなに？ - ねこすたっと

おさらい：分布を要約する

収集されたデータにおいて「変数がどのような値を取っているか」を、変数の分布と呼びます。 数値で分布を要約したり、グラフで可視化することで分布の様子を示すことができます。

ここでは数値を使って分布を要約する方法を、変数のタイプ別に見ていきましょう。

質的変数の分布を示す

同じクラスの人の血液型をまとめることを考えてみましょう。 まずは、「Ａ型が⚪︎人」というようにそれぞれの血液型の人数を集計しますよね。 このとき、値として変数に含まれる各血液型を水準（level）、それぞれの血液型の人数を度数（frequency）と言います。

当たり前ですが、全体の人数が増えればA型の度数も増えるので、その度数が大きいのか小さいのか分かりません。そこで、度数を全体数で割った割合（proportion）も示すと分かりやすいですね。表のまとめ方は下を参考にしてください。

比・割合・率

ここで用語を整理しましょう。比（ratio）とは、数を数で割ったものです。 これに対し、割合（proportion）では、割られる数（=分子）が割る数（=分母）に含まれていなくてはいけません。

例えば、男子の割合と言ったら、分子は男子の人数、分母は男女全体の人数なので、分子は分母の一部ですよね。これに対して男女比と言ったら、男子の人数を女子の人数で割ったもの*1なので、分子は分母に含まれていません。

上記の違いがわかっていれば、比は0以上、割合は0〜1の範囲の値になることが分かりますよね。

割合に代わって率という語が使われることが多いですが、区別して使う場合があるので注意しましょう。率（rate）は、ある一定期間において観察される数量を表すときに使います。数量を、時間に関係する数字で割るので、ある種の「速さ」を表していることになるのが分かるでしょうか。

例えば、「忘れ物を3回しました」と言っても、どれくらいの期間の話なのかによって意味が変わりますよね。3年間で3回なら0.083回/月ですが、3日で3回なら30回/月（多い！）です。観察期間を揃えることで比較できるというわけです。

野球の話で言えば、防御率はピッチャーが1試合あたりに取られる点数*2なので「率」で正解ですが、打率は打数のうちヒットを打った「割合」なので「率」ではありません。

量的変数の分布を要約する

中心位置

量的変数、例えば数学の点数の分布はどのように要約したらいいでしょうか。 一番気になるのは平均点ですね。平均は分布の中心位置がどこにあるかを示す要約値の1つです。

中心位置を示す指標には次のようなものがあります。

  • 平均（mean）：
    全員の点数を足して、人数で割ったもの
  • 中央値（median）：
    真ん中の人の点数。例えば、5人いたら3番目の人の点数が中央値。
  • 最頻値（mode）：
    一番頻度が多い点数。例えば、80点が5人、85点が5人、90点が10人いたら、最頻値は90点。

分布の広がり

平均点の次に気になるのは偏差値でしょうか。平均点が同じでも、点数のバラツキ具合によって偏差値は変わります（バラツキの大きいテストだと、点数が悪くても意外に偏差値は低くなかったりする）。 偏差値を計算するのに用いられる、分布の広がり具合を示す要約値は標準偏差です。バラツキの指標は次のようなものがあります。

  • 標準偏差（standard deviation, SD）：
    それぞれの人の点数と平均点の距離を全て使って計算します。平均と合わせて使います。
  • 四分位範囲（interquartile range, IQR）：
    「しぶんいはんい」と読みます。下位25%の人の点数と上位25%の人の点数を使って表します。これらの境界値は中央値と合わせて、全体を4等分する数値なので四分位数と呼びます。
  • 範囲（range）：
    最低点と最高点で表します。

実際に計算してみる

10人の点数がが次のような結果だったとしましょう。

50, 55, 58, 60, 62, 70, 72, 82, 100, 100

まず、平均mを計算すると、

\begin{aligned} m &= \frac{50 + 55 + ... + 100}{10} \\ &= 70.9 \end{aligned}

です。

標準偏差sは、各生徒の点数と平均の差の2乗を足し合わせて、人数-1で割ったものの平方根です。ちなみに、平方根を取る前、つまり s^2 は分散（variance）と呼びます。

\begin{aligned} s &= \sqrt{\frac{(50-70.9)^2 + (55-70.9)^2 + ... + (100-70.9)^2 }{10-1}} \\ &= 17.9 \end{aligned}
  • なぜ2乗したの？
    → そのまま合計するとプラスとマイナスが打ち消してゼロになるから
  • なぜ平方根を取ったの？
    → 元の測定値と単位（次元）を揃えるため
  • なぜ人数で割るのでなく、人数-1で割ったの？
    → 母集団の期待値としてはn-1で割った方が適切だから*3
  • どんなときに役に立つの？
    →標準偏差は正規分布という特別整った分布を要約するときに役に立ちます（また別の機会に説明します）

中央値Mは全体を半分ずつに分ける値なので、5位と6位の間の数値になります。この2人の点数の平均値を中央値とします。

\begin{aligned} M &= \frac{62 + 70}{2} \\ &= 66 \end{aligned}

四分位範囲は、下位1/4と上位1/4の値で表すので、10人の場合は3位と8位（それぞれ下半分・上半分の5人の真ん中）の点数から[58, 82] となります*4。

最後に、2人いる100点が最頻値となります。人数が少ないと感覚からズレやすくなる指標なので注意しましょう。

おわりに

ランキング参加中
統計

*1:逆でもOK

*2:正確には自責点

*3:難しい話なので興味ある人はこちら→分散はnで割るか n-1で割るか

*4:分位数の決め方は色々あります。知りたい人はこちら→Quantile - Wikipedia（英語）

高校生のためのデータ分析入門 (2)：変数ってなに？

elementary presentation terminology reporting

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

前回：高校生のためのデータ分析入門 (1)：まずは概要を知ろう - ねこすたっと

変数とは

数学では方程式を習うときに、変数と定数という用語が出てきたと思います。

  • 定数：問題の中で、ある値を取ることが決まっている数
  • 変数：問題の中で、制約がありながらも自由に値をとることができる数

例えば、「 y=ax^2 が(1,2)を通っている」と言われたら、aは文字で書いてあっても本当はある値（a=2）に固定されていますよね。それに対し、x, yは制約はあるものの自由に色んな値を取ることができます。この文脈でaは定数、xとyは変数です。

データ分析（というか統計学）における変数は違う観点で説明されるので、少し戸惑うかもしれません。 データ分析では、変数（variable）は収集された各項目を指します。

例えば、クラスの人の身長を測定してデータにした場合、対象者によってその値は変わりますよね。だから身長は変数です。

変数はそれぞれの対象者についての値（value）を収めている箱だと思ってください。

変数のタイプ

変数にはいくつかタイプがあって、それに応じて扱い方、つまり要約方法や使用するグラフが変わります。

量的変数

量的変数（quantitative variable）とは、量や個数を値に取る変数です。

例：身長、時間の長さ、入場者数

数字で表されるので、合計したり平均を計算したりすることができます。

質的変数

質的変数（qualitative variable）とは、性質を表す値を取る変数です。カテゴリー変数（categorical variable）と呼ぶこともあります。

例：血液型、虹彩の色、人種

質的変数が取る値は、だいたいは文字を使って表されます（例：A型、B型など）が、数字を使っていても質的変数のことがあるので注意です。例えば、1組の子が2人、2組の子が2人いるからといって、「その4人の平均は1.5組である」とは言いませんね。

「あり・なし」や「勝ち・負け」のように、カテゴリーの数が2種類しかないものを2値変数（dichotomous variable）と呼びます。質的変数の中でも使う頻度が多いので特別に名前がついてます。

もっと詳しい分類方法が知りたかったら、下の記事を読んでみてください。

変数の型と測定尺度の分類 - ねこすたっと

変数の分布を示す

対象集団において、変数がどんな値を取っているか、どんなふうにバラついているか、を変数の分布（distribution）と言います。 変数がどのように分布しているかを見ることは、データ分析の基本のキです。

「このクラスの数学の点数は、90点が1人、88点が3人、85点が…」と説明されても、全体の様子が分かりませんよね。全員分の点数を聞かなくても、平均点や再試験の割合を聞けばだいたいの様子はつかめます。

分布を数値で要約する以外にも、グラフを使って分布を可視化することで全体の様子がよく分かります（下のグラフで赤線は平均点）。

おわりに

ランキング参加中
統計

高校生のためのデータ分析入門 (1)：まずは概要を知ろう

elementary

数学が苦手なうちのJKに、将来必要となるかもしれないデータ分析への抵抗感をなくしてもらう目的で記事を書くことにしました。

データとは

日常的によく使われている「データ（data）」という用語の意味を、改めて考えようとすると結構奥が深いです。

データは「物事の性質を表すために与えられた数値や記号」です。この記号そのものにはまだ意味がありません。解析して解釈して初めて意味や価値が与えられます（詳細は下のリンクを参照）。

例えば、

  • クラスの全員の身長（cm）：181, 190, 210, ...
    → 数値が並んでいるだけ。ただの「データ」。
  • クラスの平均身長：191cm（日本人の平均よりもだいぶ高そうだ）
    → 分析することで解釈され、意味のある「情報」になった！

データにした段階で情報は失われている

これは、記録した紙を捨てちゃったとか、パソコンが壊れちゃったとか、そういう話ではありません。 データ収集は、物事の性質を捉えるために色々と測定して数値・記号にするプロセスですが、データにした段階で捉えたい性質の一部は必ず失われている、という話。

例えば、果物の色という特徴をデータとして測定するとします。リンゴなら赤とか緑（ときに黄色？）でしょうかね。でも、リンゴの色を「赤」とした時点で、赤の濃さとか色のムラとかいう情報は抜け落ちます。 色の表現をもっと増やせば、拾える情報は増えるかもしれませんが、もとのリンゴの色の情報を完全に再現しようとすれば、元のリンゴを完コピすることになってしまいます。 特徴をデータにして解析・解釈することが目的なので、ある程度単純化しないといけない。完コピでは意味がなくなっちゃいます。

ちなみに、解釈する段階でも情報は削ぎ落とされます（簡単にしないと人間が解釈できないから）。その話はまた今度。

データ分析の目的を分類してみる

何のためにデータを分析するのかと言えば、「何かを決断するときの根拠が欲しいから」でしょう。

例えば、

  • このお客さんに何をすすめたら買ってくれるかな
  • この商品を来月はどれくらい仕入れようか
  • この患者さんにはどちらの治療法が効果が高いだろうか

など、色んな決断をするときに、勘や雰囲気よりももっと客観的な根拠が欲しいですよね。

難しい言い方をすれば、データ分析の目的は、根拠となりうる情報を提供して意思決定を支援することだと言えます。 ただ、それだけだと広すぎてつかみどころがないので、もう少し細かく分類してみます。

1. 特徴を発見する

数字・記号の羅列を見ていても、なかなか全体の特徴は分かりません。平均とか標準偏差とかを使ってデータを要約することで、対象全体の特徴がつかみやすくなります。

数値で要約すると、ノイズを落として特徴を見えやすくできる反面、大事な特徴も落としてしまうこともあります。こんなときはグラフを使う方がいいです。

例えば、下のグラフでは2つの山がありますが、平均値（赤線）は谷にある。つまり、全体の少数派の値が全体を代表してしまっています。

2. 似たグループを探す

データが似たもの同士のグループを探すことをクラスタリング（clustering）と呼んだりします（クラスター = かたまり）。

数値で要約することが、対象全体を1つにまとめてしまうことが目的だったのに対し、クラスタリングは対象を複数のグループに分けることが目的です。さっきのグラフで言えば、山を作っていた2つのグループに分けることです。

3. 予測する

将来のことが分かったら、めちゃめちゃ役に立ちます。 どれくらい商品が売れるか予測できれば無駄が出ないように仕入れ数を決めることができますし、病気になるかどうか予測できればリスクが高い人に何かできることがあるかもしれない。

予測（prediction）というと、普通は過去〜現在のデータを使って、未来を言い当てることを思い浮かべますが、現在のデータで現在のことを言い当てることも「予測」です。 例えば、ある病気かどうかを調べるためにはすごく痛い検査をしないといけない場合、簡単な検査で正解を言い当てられたら便利ですよね。

臨床研究だと、前者を予後予測（prognostic prediction）、後者を診断予測（diagnostic prediction）と言ったりします。

4. 介入の効果をみる

例えば、ヘルメットを被るとどれくらい死亡事故を減らせるのかとか、YouTubeで広告を出したらどれくらい売り上げが伸びたのか、といった状況です。「ヘルメットを装着させる」や「広告を出す」のように、何かを与えたり、やらせたりすることを介入（intervention）と言います。

やった場合とやってない場合を比べることで介入の効果をみます（比較が大事）。ただし、介入以外の条件が同じであることが前提です。 例えば、売り上げが右肩上がりの状態で広告の前後を比較しても、広告の効果なのか（シナリオ1）、自然に増えただけなのか（シナリオ2）分かりませんよね。

5. 測定方法を評価する

何かを測定した結果が正しくなければ、データそのものが無意味になってしまいます。次のような項目を評価します。

  • 信頼性（reliability）：
    同じ条件下で測定を繰り返したときに、一貫した結果が得られるか
  • 識別性（discriminability）：
    測定結果によって異なった状態を区別できるか。例えば、ある検査の結果をもとにして、本当に病気があるかどうかをどれくらい言い当てられるか。*1
  • 妥当性（validity）：
    測定方法が測定しようとしている特性を正確にとらえられているか。例えば、抱えるストレスを新しい心理テストで測定したとき、新しいテストのスコアが他のストレステストの結果やストレスに関連する身体症状と関連があれば、新しいテストの妥当性は高いと考えられる。

おわりに

  • 「データ分析とは何か」と偉そうなことを書いたけど、私は研究以外で使った経験はほとんどありません。
  • データ分析にもとづいて仕事の課題を解決するためには、上司や同僚に分析結果を分かってもらわないといけなかったり、業務に取り入れるときのコストやリスクを考える必要があったりと、他にもハードルがたくさんあります。なので、客観的に考えるためにはデータ分析は必要だけど、それだけで全てが解決するとは思わない方がいいです。
  • 次回： 高校生のためのデータ分析入門 (2)：変数ってなに？ - ねこすたっと

ランキング参加中
統計

*1:予測能の評価にも使う

ZoteroをWebDAV経由で同期させて資料を管理する

zotero neco

以前、Dropbox経由でZoteroを同期させる方法をまとめました。

necostat.hatenablog.jp

この方法だとPDFしか同期できず、Webページやパワポは別の方法で管理しなくてはなりませんでした。 WebDAV（ウェブダブ）経由で同期させる方法だと解決したので、備忘録としてまとめておきます。

ファイル転送とかネットワークセキュリティとかに疎い者が書いてます。用語など間違ってたらごめんなさい。

Zoteroの仕組みを理解する

以前の記事では、Zoteroの仕組みをあまり理解しないまま、設定方法だけをまとめました。 今回はZoteroについて、もう少し理解するよう努めます。

アイテム / コレクション / ライブラリ

Zoteroで管理される個々の収集物を「アイテム」と呼びます。

PDFなどの収集されたデータは単独のアイテムとして保存しておくこともできますが、通常はメタデータ（コンテンツの種類や文献情報、タグなどに関するデータ）を含んでいる親アイテムに付属する子アイテムとして保存します（せっかくZoteroを使うんだから、分類・整理に役立つ情報とくっつけておく方が便利！）。

下の例だと、文献のメタデータを含んだ親アイテムの下に、自作メモと文献PDFが子アイテムとして保存されています（実際は、メモは使い勝手が合わないのでほとんど使っていません...）。

Zoteroではアイテムをコレクションとタグを使って整理します。上の例のように、コレクションは階層化できます。一見フォルダ管理のように見えますが、アイテムは複数のコレクションに所属することができるので、「コレクション = 階層化できるタグ」と言えると思います。

自分が保存しているアイテムの集合がマイ・ライブラリです。これに加えて、研究室などのグループ内で他の人が保存しているアイテムを共有することも出来ます（ただし、無料では同期容量制限あり）。

データとファイルの同期

Zoteroは複数の端末で同期することができます*1。こうすることで、自宅のPCで保存した資料が職場のPCでも閲覧できたり、PCで保存した文献をiPadで読んだりすることができます。

アイテムの同期は、

  • データ同期
  • ファイル同期

の2つで構成されています。

データ同期（Data Syncing）は、文献情報などのメタデータ、タグ、メモといった添付ファイル以外の同期です。ZoteroアカウントでZoteroサーバーにログインすることで、無料・無制限に行われます*2。

ファイル同期（File Syncing）は、文献PDFなどの本体ファイルの同期です。Zoteroサーバーを介して本体ファイルの同期を行うことも可能ですが、300MBを超える場合は有料プランへの加入が必要です。

300MBは使い切るまであっという間ですね。何事もなるべく無料の範囲でやりたい私としてはZoteroサーバーを介さない方法を選ばなくてはなりません。

1つ目の方法は、ファイル本体の同期はDropbox（などクラウドストレージ）を使い、ZotFileというアドオンを使って本体ファイルへのリンクを同期する方法です。リンク情報の共有ならデータ同期に含まれるので無料・無制限です（多分）。

Dropboxを使ったファイル同期

2つ目の方法は、WebDAVを使う方法です。WebDAVはHTTPを拡張して、ファイルのやりとりができるようにした技術・機能です。これを使えば複数の端末でファイルを共有することができます。

WebDAVを使ったファイル同期

WebDAV機能を使うには、Webサーバー*3を用意する必要があります。 レンタルサーバーを借りるとなると敷居が高いですが、WebDAVを提供しているクラウドストレージサービスを使えば比較的簡単です。

私も今のところInfiniCLOUDというクラウドストレージを使っています*4が、総容量が増えてきたらNASに移行予定です。

WebDAVを使ってファイル同期させる

InfiniCLOUDの設定

下のリンクからInifniCLOUDのトップページに行って、無料アカウントを作成します。20GBなので文献PDFだけなら結構入りそうです。

マイページに進みます。

真ん中あたりにある「外部アプリ接続を許可する」にチェックを入れます。アプリパスワードが表示されなければ再発行ボタンを押してください。

ページを閉じた後にパスワードを再度確認しようとしても、表示のためには再発行が必要になりますので注意してください。 WebDAV接続URL（https://wani.teracloud.jp/dav/）も後で必要になります。

ちなみに、その下に紹介コードが表示されます。私のはP4JZYでしたので、よかったらどうぞ（笑）

Zoteroの設定（PC）

Zoteroの「環境設定」から「同期」の設定へ進みます。

データ同期のユーザー名には、Zoteroのアカウントを入力します。

「マイ・ライブラリ内の添付ファイルの同期には右のプログラムを使う」は「WebDAV」を選択します（「Zotero」での無料の同期は300MBまで）。 「URL」にInfiniCLOUDの設定でメモったWebDAV接続URLを、「ユーザー名」にInfiniCLOUDのユーザー名を、「パスワード」にInfiniCLOUDで発行されたパスワードをそれぞれ入力します。

「サーバーを検証する」ボタンを押して同期に成功したというメッセージが出ればOKです。

ちなみに、その下にある「Zoteroストレジを利用してグループ・ライブラリの添付ファイルを同期する」は、グループでアイテムを共有しない限り関係ありません。

Zoteroの設定（iOSアプリ）

iPhoneやiPadで文献を読みたい人向けに、iOS版もあります。

Zotero

Zotero

  • Zotero
  • 仕事効率化
  • 無料
apps.apple.com

右上の歯車マークを押して設定画面に進みます。

英語表記ですが、DATA SYNCING（データ同期）、FILE SYNCING（ファイル同期）が分かればPC版と同じように設定できると思います。

おわりに

  • WebDAVではグループ・ライブラリの共有ができません。研究室などで共有したいときは諦めてZoteroを有料アップグレードしましょう。
  • 飼い猫がストルバイト結石になってしましました。

ランキング参加中
統計

ドクターズケア (Dr's CARE) 療法食 猫用 ストルバイトケア チキンテイスト 400g×4袋

ドクターズケア (Dr's CARE) 療法食 猫用 ストルバイトケア チキンテイスト 400g×4袋

  • ドクターズケア (Dr's CARE)
Amazon

*1:Zoteroは同期してナンボです。同期しなかったらメリット半減どころか9割減です。

*2:メモの中に添付された画像は同期容量を喰います（多分）

*3:図中では分かりやすさを優先してWebDAVサーバーと書きましたが、この用語が適切かどうか分かりません

*4:DropboxなどメジャーなクラウドストレージはWebDAV機能を提供していません。Boxは以前提供していたそうですが、今はサポート終了のようです。

分散分析（ANOVA）：球面性仮定

testing clustered/repeated maths/theory neco

分散分析で満たすべき仮定として球面性の仮定（the assumption of sphericity）*1をよく目にしますが、きちんと勉強したことがなかったので（わかるところだけ）読んでみました。

分散分析に必要な仮定

異なる対象者同士で比較する被験者間分散分析（between-subjects ANOVA）には、

  • 観測が互いに独立である（independence of observations）
  • 各群内で正規分布している（normality）
  • 各群の分散が等しい（homogeneity of variance）

の3つの仮定が必要です。

同じ対象者に対して観察された値同士を比較する 被験者内分散分析（within-subjects ANOVA） 、あるいは反復測定分散分析（repeated measures ANOVA） では、上記に加え 球面性の仮定（the assumption of sphericity） が必要になります。

球面性の仮定は反復測定ANOVAにおいてF値が正確なF分布に従うための必要十分条件で、これが満たされていないと第1種過誤が増加してしまい*2、ANOVAの結果が不適切になってしまいます。

球面性の仮定とは

Lane (2016) の導入で、球面性について2通りの定義を紹介していました。

  • 2水準間の差の分散に基づいた定義方法
  • 直交対比（orthogonal contrast）の分散・共分散に基づいた定義方法

両者は同値ですが、前者の方が説明が分かりやすく、後者の方が一般化して複雑なデザインにも対応できます。

2水準間の差の分散に基づいた定義方法

要因に含まれる全ての2水準間について対象者内の差を計算し、その分散が全て等しいとき、球面性が満たされていると定義します。 下の表では、T1〜T3の3つの水準の差（T3-T2, T3-T1, T2-T1）を計算して、その分散が全て等しい値（=8）になっていることを示しています。 ちなみに分散分析では各群の分散が等しくなければいけないので、T1〜T3の分散も全て等しい値（=10）になっていることを示しています。

]

水準が2つしかない場合（例えば前値・後値を測定）、水準間差は1つしか存在しないので、「水準間によって分散が異なっている」という事態は発生せず球面性は常に成り立ちます。

直交対比の分散・共分散に基づいた定義方法

多重比較の手順の1つであるSchefféの方法で対比（contrast）が登場します。複数の平均値（例えば \mu_1, \mu_2, \mu_3, \mu_4）を比べるとき、任意の平均の比較は \mu_1, \mu_2, \mu_3, \mu_4の線型結合が0であるという形式で表すことができます。

例えば「1番目と2番目の平均が等しい」、つまり \mu_1 = \mu_2 という仮説は、

1 \times \mu_1 + (-1) \times \mu_2 + 0 \times \mu_3 + 0 \times \mu_4 = 0

と書けますし、「1番目の平均と他の3つの平均の平均が等しい」、つまり \mu_1 = \frac{\mu_2 + \mu_3 + \mu_4}{3} という仮説は、

1 \times \mu_1 + \left( -\frac{1}{3} \right) \times \mu_2 + \left( -\frac{1}{3} \right) \times \mu_3 + \left( -\frac{1}{3} \right) \times \mu_4 = 0

と書けます。

この線型結合の係数を 対比（contrast） といいます（各係数を要素に持つベクトルです）。

2つの対比が直交する（=内積が0）とき、この2つの対比は直交対比（orthogonal contrast）であると言います。 分散分析の帰無仮説である「p個の平均が全て等しい」、つまり \mu_1 = \mu_2 = ... = \mu_pという仮説は、「p-1個の直交対比が全て0である」という仮説に置き換えることができます（p-1個の直交対比の選び方は無数にありますが、互いに直交する対比は常にp-1個しか作れません）。

このp-1個の直交対比ベクトル（←各々がp個の要素からなる）を並べた(p-1)×p行列を直交対比行列（orthogonal matrix）と言います。 さらに、

  • 各行の和 = 0
  • 各行の長さ（平方和）= 1

という条件が追加されたものを正規直交対比行列（orthonormal contrast matrix）と言います。

元のデータの共分散行列 \Sigma を正規直交対比行列 C を使って、 C \Sigma C^{T} と変換したものが、対角成分が全て等しい対角行列 \lambda Iになっているというのが球面性の仮定です。

C \Sigma C^{T} = \lambda I

\Sigma = E(X^{T} X) を鑑みてさらに読み砕くと、

元データXを正規直交対比行列で変換した X C^{T} の分散が等しく、かつ互いに相関がない というのが球面性の仮定の意味するところです。

直交対比に基づいた球面性の仮定については、名古屋大学大学院 教育発達科学研究科 心理発達科学専攻 計量心理学領域 石井研究室が公開している資料集を参考にしました。非常に分かりやすい資料でとても勉強になりましした。

検定方法

Mauchly（モクリー）の球面性検定がよく知られています。Mauchlyの統計量Wは0（球面性が成り立たない）〜1（完全に球面性OK）の値を取り、仮説が棄却された（P値が小さい）場合は球面性が成り立っていないと判断します。

もし被験者内要因（=反復測定要因）に加えて、被験者間要因を含むデザインでは、共分散行列が群ごとで等質かどうかを検証しなくてはなりません。Mauchly検定はこれに対応していません。球面性と共分散の等質性を一度に検定する方法としてMendozaの多標本球面性検定があります。

これについては井関先生が詳しく解説されています（井関先生が作成されたR関数ANOVA君ではMendoza検定がデフォルトになっているとのこと）。

riseki.php.xdomain.jp

球面性仮定が満たされなかったときの補正方法

球面性仮定が満たされていない場合、計算されたF値がF分布に従うとみなせなくなるので調整が必要です。ε統計量を使って分散分析の自由度を調整します。

データから計算されたF値をF(df1, df2)分布に当てはめてP値を計算するのではなく、F(ε×df1, ε×df2)分布に当てはめて計算します。当てはめるF分布の自由度が小さいほど計算されるP値は大きくなります。

ε統計量の計算方法はいくつかあります。いずれも0〜1の範囲で求められ、球面性が成り立っていないときほど0に近い値になるので、自由度は調整前よりも小さくなり、P値は調整前よりも大きくなります。

  • 下限値：εの取りうる理論的下限値です。1/(水準数-1)で計算できるのでPC不要ですが、保守的過ぎるので通常使いません。
  • Greenhouse-Geisser法*3：ε≧0.75のときには厳し過ぎるとのこと
  • Huynh-Feldt法*4：計算上1を超えることがありますが、その場合は1を用います。Lecoutre（ルクルト）による修正版が用いられていることが多く、Huynh-Feldt-Lecoutre法と呼ぶ方が良いかもしれません。
  • Chi-Muller法：計算上1を超えることも、下限値よりも小さい値になることもあるとのこと。GG法、HFL法の使い分けを気にせず、広い状況で優れている？

使い分けの詳細はまだ勉強しきれていません。ひとまずは

  • ε<0.75 → Greenhouse-Geisser法
  • ε≧0.75 → Huynh-Feldt-Lecoutre法

とざっくり覚えておきたいと思います。

おわりに

  • 理解という意味ではまだまだですが、出力された表に何が書いてあるかは分かるようになりました。
  • 猫の爪研ぎタワーから毎日大量のゴミが出ます。麻紐がとれて芯が剥き出しです。

ランキング参加中
統計

参考資料

  • Lane, D. M. (2016). The assumption of sphericity in repeated-measures designs: what it means and what to do when it is violated. The Quantitative Methods for Psychology, 12(2), 114–122. doi:10.20982/tqmp.12.2.p114

  • 千野直仁. 行動研究における反復測定デザインANOVAの誤用 - I. 愛知学院大学心身科学部紀要第9号（45-52）(2013).

  • EZR, SPSSでの実行方法なども紹介されています。

toukeier.hatenablog.com

*1:千野（2013）によると「球面性」ではなく「球形」とすべきと言われています。「表面だけでなく球内部も分布しているから」という理由で納得しましたが、ここでは検索へのかかりやすさの観点から「球面性」としました。

*2:差がないのに有意差ありとしてしまう

*3:グリーンハウス・ガイサーと読むそうです

*4:フィン・フェルトと読むそうです