分散分析で満たすべき仮定として球面性の仮定(the assumption of sphericity)*1をよく目にしますが、きちんと勉強したことがなかったので(わかるところだけ)読んでみました。
分散分析に必要な仮定
異なる対象者同士で比較する被験者間分散分析(between-subjects ANOVA)には、
- 観測が互いに独立である(independence of observations)
- 各群内で正規分布している(normality)
- 各群の分散が等しい(homogeneity of variance)
の3つの仮定が必要です。
同じ対象者に対して観察された値同士を比較する 被験者内分散分析(within-subjects ANOVA) 、あるいは反復測定分散分析(repeated measures ANOVA) では、上記に加え 球面性の仮定(the assumption of sphericity) が必要になります。
球面性の仮定は反復測定ANOVAにおいてF値が正確なF分布に従うための必要十分条件で、これが満たされていないと第1種過誤が増加してしまい*2、ANOVAの結果が不適切になってしまいます。
球面性の仮定とは
Lane (2016) の導入で、球面性について2通りの定義を紹介していました。
- 2水準間の差の分散に基づいた定義方法
- 直交対比(orthogonal contrast)の分散・共分散に基づいた定義方法
両者は同値ですが、前者の方が説明が分かりやすく、後者の方が一般化して複雑なデザインにも対応できます。
2水準間の差の分散に基づいた定義方法
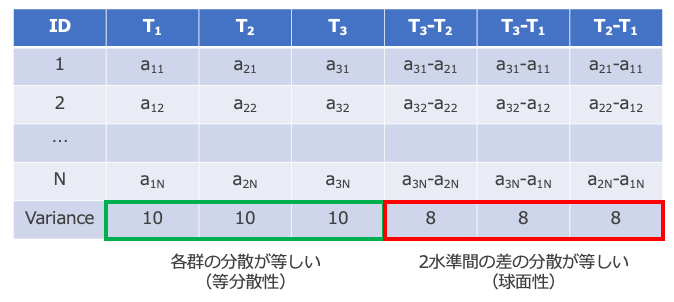
要因に含まれる全ての2水準間について対象者内の差を計算し、その分散が全て等しいとき、球面性が満たされていると定義します。 下の表では、T1〜T3の3つの水準の差(T3-T2, T3-T1, T2-T1)を計算して、その分散が全て等しい値(=8)になっていることを示しています。 ちなみに分散分析では各群の分散が等しくなければいけないので、T1〜T3の分散も全て等しい値(=10)になっていることを示しています。
 ]
]
水準が2つしかない場合(例えば前値・後値を測定)、水準間差は1つしか存在しないので、「水準間によって分散が異なっている」という事態は発生せず球面性は常に成り立ちます。
直交対比の分散・共分散に基づいた定義方法
多重比較の手順の1つであるSchefféの方法で対比(contrast)が登場します。複数の平均値(例えば)を比べるとき、任意の平均の比較は
の線型結合が0であるという形式で表すことができます。
例えば「1番目と2番目の平均が等しい」、つまり という仮説は、
と書けますし、「1番目の平均と他の3つの平均の平均が等しい」、つまり という仮説は、
と書けます。
この線型結合の係数を 対比(contrast) といいます(各係数を要素に持つベクトルです)。
2つの対比が直交する(=内積が0)とき、この2つの対比は直交対比(orthogonal contrast)であると言います。
分散分析の帰無仮説である「p個の平均が全て等しい」、つまりという仮説は、「p-1個の直交対比が全て0である」という仮説に置き換えることができます(p-1個の直交対比の選び方は無数にありますが、互いに直交する対比は常にp-1個しか作れません)。
このp-1個の直交対比ベクトル(←各々がp個の要素からなる)を並べた(p-1)×p行列を直交対比行列(orthogonal matrix)と言います。 さらに、
- 各行の和 = 0
- 各行の長さ(平方和)= 1
という条件が追加されたものを正規直交対比行列(orthonormal contrast matrix)と言います。
元のデータの共分散行列 を正規直交対比行列
を使って、
と変換したものが、対角成分が全て等しい対角行列
になっているというのが球面性の仮定です。
を鑑みてさらに読み砕くと、
元データXを正規直交対比行列で変換した の分散が等しく、かつ互いに相関がない というのが球面性の仮定の意味するところです。
直交対比に基づいた球面性の仮定については、名古屋大学大学院 教育発達科学研究科 心理発達科学専攻 計量心理学領域 石井研究室が公開している資料集を参考にしました。非常に分かりやすい資料でとても勉強になりましした。
検定方法
Mauchly(モクリー)の球面性検定がよく知られています。Mauchlyの統計量Wは0(球面性が成り立たない)〜1(完全に球面性OK)の値を取り、仮説が棄却された(P値が小さい)場合は球面性が成り立っていないと判断します。
もし被験者内要因(=反復測定要因)に加えて、被験者間要因を含むデザインでは、共分散行列が群ごとで等質かどうかを検証しなくてはなりません。Mauchly検定はこれに対応していません。球面性と共分散の等質性を一度に検定する方法としてMendozaの多標本球面性検定があります。
これについては井関先生が詳しく解説されています(井関先生が作成されたR関数ANOVA君ではMendoza検定がデフォルトになっているとのこと)。
球面性仮定が満たされなかったときの補正方法
球面性仮定が満たされていない場合、計算されたF値がF分布に従うとみなせなくなるので調整が必要です。ε統計量を使って分散分析の自由度を調整します。
データから計算されたF値をF(df1, df2)分布に当てはめてP値を計算するのではなく、F(ε×df1, ε×df2)分布に当てはめて計算します。当てはめるF分布の自由度が小さいほど計算されるP値は大きくなります。
ε統計量の計算方法はいくつかあります。いずれも0〜1の範囲で求められ、球面性が成り立っていないときほど0に近い値になるので、自由度は調整前よりも小さくなり、P値は調整前よりも大きくなります。
- 下限値:εの取りうる理論的下限値です。1/(水準数-1)で計算できるのでPC不要ですが、保守的過ぎるので通常使いません。
- Greenhouse-Geisser法*3:ε≧0.75のときには厳し過ぎるとのこと
- Huynh-Feldt法*4:計算上1を超えることがありますが、その場合は1を用います。Lecoutre(ルクルト)による修正版が用いられていることが多く、Huynh-Feldt-Lecoutre法と呼ぶ方が良いかもしれません。
- Chi-Muller法:計算上1を超えることも、下限値よりも小さい値になることもあるとのこと。GG法、HFL法の使い分けを気にせず、広い状況で優れている?
使い分けの詳細はまだ勉強しきれていません。ひとまずは
- ε<0.75 → Greenhouse-Geisser法
- ε≧0.75 → Huynh-Feldt-Lecoutre法
とざっくり覚えておきたいと思います。
おわりに
- 理解という意味ではまだまだですが、出力された表に何が書いてあるかは分かるようになりました。
- 猫の爪研ぎタワーから毎日大量のゴミが出ます。麻紐がとれて芯が剥き出しです。
参考資料
Lane, D. M. (2016). The assumption of sphericity in repeated-measures designs: what it means and what to do when it is violated. The Quantitative Methods for Psychology, 12(2), 114–122. doi:10.20982/tqmp.12.2.p114
千野直仁. 行動研究における反復測定デザインANOVAの誤用 - I. 愛知学院大学心身科学部紀要第9号(45-52)(2013).
EZR, SPSSでの実行方法なども紹介されています。