分散分析（ANOVA）：平方和と自由度の分割

分散分析（Analysis of Variance, ANOVA）を学ぶ目的でKutner先生のApplied Linear Statistical Models（5th edition）を拾い読みし始めました。今回は主に"Chapter 16： Single Factor Studies" から、分散分析の基本となる平方和・自由度の分割についてです。

ANOVAとは
- セル平均モデル（cell means model）
平方和の分割
- 平方和とは
- 群間の平方和と郡内の平方和に分ける
自由度の分割
- 自由度とは
- 自由度も群間と郡内に分ける
平均平方
分散分析表
おわりに

ANOVAとは

似たもの同士を同じグループに分類すれば、グループ内は分ける前の全体の状態と比べて均一に近づきます。意味のある分け方をすれば、バラツキを減らすことができるということです。別の言い方をすれば、分類してバラツキが減らせたということは、対象物の特性について知ることができたということです。

ANOVAとはデータをグループに分類する（群分けする）ことでバラツキが減るかどうかを検証する方法です。ある変数で分類することでバラツキが統計的に有意に減ったのであれば、その変数はデータの特徴の一部を説明できているだろう、というロジックです。

例えば、下の図の場合はグループ分けすることでバラツキが減っているので、意味のある分類と言えます。

一方、下の図の場合はグループ分けしてもほとんどバラツキは変わっていませんので、この分類はデータの特徴の説明に役に立っていないと言えます。

群分けの方法は、割り付ける治療のように研究者が決めることもできますし、対象にそもそも備わっている特性で分類することもできます。なのでグループの呼び方は「群」の他に、治療あるいは処理（treatment）や、要因（factor）など文脈によって様々です。

セル平均モデル（cell means model）

ANOVAも回帰と同様に解析の際にモデルを想定しますが、セル平均モデルは最もシンプルなものです。

$\begin{aligned} Y_{ik} &= \mu_i + \varepsilon_{ik} \\ \varepsilon_{ik} &\sim Normal(0, \sigma ^2) \\ \varepsilon_{ik} &\perp \varepsilon_{i'k'} \end{aligned}$

1つ目の式において、 $Y_{ik}$ はi番目の治療（要因）群に属するk番目の観測値を表しています。右辺の $\mu_i$ はi番目の群の真の平均を表すパラメータ、 $\varepsilon_{ik}$ は真の平均と観測値との間の誤差です。

2つ目の式では、誤差が正規分布に従うことを示しています。属する群にかかわらず全ての誤差の分散は同じと想定されます。

3つ目の式では、それぞれの誤差が互いに独立であることを示しています。

変数が2つに増えると、それぞれの治療（要因）の効果を加法性や交互作用についての仮定が登場します。また、群を決める変数が量的変数の場合は、群平均 $\mu_i$ と変数 $i$ の間に関数を想定して回帰モデルと考えることもできます*1。

平方和の分割

平方和とは

バラツキ具合の指標として、平方和（sum of squares, SS*2）を用います。平方和とは、平均と観測値との差の2乗（偏差平方）を足し合わせたものです。単純に平均と観測値との差を足し合わせると正負打ち消しあって0になってしまうので2乗してから足しています。

例えば、a種類の治療があって、いずれの治療群にもn個の観測値が属するとします。このときの総平方和（total sum of squares, SSTO）は、次の式で表されます。

$\begin{aligned} \sum_{i=1}^a \sum_{k=1}^n (Y_{ik} - \bar{Y}_{..})^2 \end{aligned}$

ここで、 $\bar{Y}$ は平均を表しています。右下についている".."は「iについてもkについても特定のものを想起しない」という意味です。平均なのでkについて考えないのは当たり前ですが、「iも特定しない」としているので、 $\bar{Y}_{..}$ は群を分けない全体の平均であることを意味しています。逆に $\bar{Y}_{i.}$ と書けば治療群は特定しているので、i番目の治療群の平均値となります。

Σの添字を簡略化して、

$\begin{aligned} \sum_{i} \sum_{k} (Y_{ik} - \bar{Y}_{..})^2 \end{aligned}$

と書いたり、（文脈上誤解がなければ）添字を省いたりすることもあります。

群間の平方和と郡内の平方和に分ける

i番目の治療群に属するk番目の観測値と全体平均との差を、次のように分解してみます。単にi番目の治療群に属する観測値の平均 $\bar{Y}_{i.}$ を足して引いただけです。

$\begin{aligned} Y_{ik} - \bar{Y}_{..} = (Y_{ik} - \bar{Y}_{i.}) + (\bar{Y}_{i.} - \bar{Y}_{..}) \end{aligned}$

両辺2乗します。

$\begin{aligned} \sum_{i} \sum_{k} (Y_{ik} - \bar{Y}_{..})^2 &= \sum_{i} \sum_{k} [(Y_{ik} - \bar{Y}_{i.}) + (\bar{Y}_{i.} - \bar{Y}_{..})]^2 \\ &= \sum_{i} \sum_{k} [(Y_{ik} - \bar{Y}_{i.})^2 + 2(Y_{ik} - \bar{Y}_{i.})(\bar{Y}_{i.} - \bar{Y}_{..}) + (\bar{Y}_{i.} - \bar{Y}_{..})^2] \\ &= \sum_{i} \sum_{k} (Y_{ik} - \bar{Y}_{i.})^2 + 2\sum_{i} \sum_{k}(Y_{ik} - \bar{Y}_{i.})(\bar{Y}_{i.} - \bar{Y}_{..}) + \sum_{i} \sum_{k}(\bar{Y}_{i.} - \bar{Y}_{..})^2 \end{aligned}$

第2式は展開しただけ、第3式はΣを分配しただけです。

3行目の第2項において、 $(\bar{Y}_{i.} - \bar{Y}_{..})$ はkについて和を取るときは定数なので、Σの前に出すことができます（下式）。

$\begin{aligned} \sum_{i} \sum_{k}(Y_{ik} - \bar{Y}_{i.})(\bar{Y}_{i.} - \bar{Y}_{..}) = \sum_{i} (\bar{Y}_{i.} - \bar{Y}_{..}) \sum_{k}(Y_{ik} - \bar{Y}_{i.}) \end{aligned}$

ここで、 $\sum_{k}(\bar{Y}_{ik} - \bar{Y}_{i.})$ は平均と観測値の差を2乗せずに足し合わせているので0になり、第2項は消えます。

また、i番目の治療群に属する観測数を $n_i$ とすると、

$\begin{aligned} \sum_{i} \sum_{k}(\bar{Y}_{i.} - \bar{Y}_{..})^2 = \sum_{i} n_i (\bar{Y}_{i.} - \bar{Y}_{..})^2 \end{aligned}$

となります（ $(\bar{Y}_{i.} - \bar{Y}_{..})$ は $n_i$ 個の観測に対して共通だから）。

以上をまとめると、

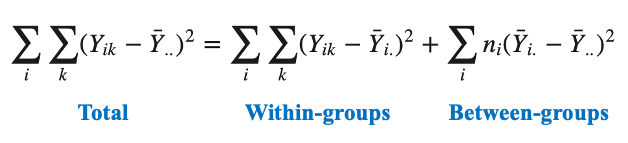
となります。

右辺第1項は「個々の観測値とそれが属する群の平均の差の平方和」なので、群内平方和と言います。グループ分けによって、群内は同じようなものの集まりとみなされることになるので、群内のバラツキは偶然誤差に起因すると考えられますので、群内平方和（sum of squares within groups）誤差平方和（error sum of squares, SSE）あるいは残差平方和（residual sum of squares, RSS）と呼ばれます。*3

右辺第2項は「群平均と全体平均の差の平方和」なので、群間平方和（sum of squares between groups）と呼ばれます。こちらは群の名前によって、当てられる略号は色々です（例：要因A→SSA, 治療→treatment sum of squares, SSTR）

自由度の分割

自由度とは

自由度（degree of freedom, df）は、変数の中で自由に値を決めることができる数のことです。例えば、3つの数a, b, cとその平均値mがあるとします。変数は4つですが、3つが決まると残りの1つの値は自動的に決まるので、この場合の自由度は3ということになります。

例として、r種類の治療があって、それぞれの治療群に $n_i$ 個の観測値が属していて、総観察数は $n_T$ とします。ここで総平方和の自由度を考えてみます。

足し合される偏差平方は $n_T$ 個ありますが、偏差となる平均を求めるために自由度を1つ使うので、総平方和の自由度は $n_T -1$ となります。

自由度も群間と郡内に分ける

平方和と同様に、自由度も群間と群内に分けてみましょう。

まず、群内の平方和では、 $n_T$ 個の偏差平方と、基準となるr個の群平均があるので、自由度は $n_T-r$ となります。次に群間の平方和では、r個の群平均とそれらの偏差の基準となる全平均が1個あるので、自由度は $r-1$ となります。

まとめると、

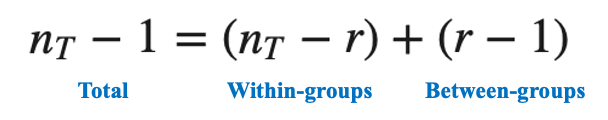
となり、自由度についても群内・群間に分けることができました。

平均平方

平方和を自由度で割ったものを平均平方（means square, MS*4）といいます。

誤差平均平方（mean square error, MSE）は誤差平方和（SSE）を自由度 $n_T-r$ で割ったものなので、

$\begin{aligned} MSE &= \frac{1}{n_T-r} \sum_{i} \sum_{k} (Y_{ik} - \bar{Y}_{i.})^2 \\ &= \frac{1}{n_T-r} \sum_{i} \left[ (n_i-1) \sum_{k} \frac{(Y_{ik} - \bar{Y}_{i.})^2}{n_i-1} \right] \end{aligned}$

ここでi番目の群の標本分散を $s_i ^2$ と書くと、

$\begin{aligned} s_i^2 = \sum_{k} \frac{(Y_{ik} - \bar{Y}_{i.})^2}{n_i-1} \end{aligned}$

であり、各群の真の分散が等しく $\sigma ^2$ であると仮定すれば、 $s_i ^2$ は $\sigma ^2$ の不偏推定量（ $E \{s_i ^2 \} = \sigma ^2$ ）なので、

$\begin{aligned} E \{MSE\} &= \frac{1}{n_T-r} \sum_{i} (n_i-1) E \{ s_i ^2 \} \\ &= \frac{1}{n_T-r} \sum_{i} (n_i-1) \sigma ^2 \\ &= \frac{\sigma ^2}{n_T-r} \sum_{i} (n_i-1) \\ &= \sigma ^2 \end{aligned}$