Bland-Altmanプロットで測定の一致性を評価する（BlandAltmanLehパッケージ）[R]

Agreementの評価として相関係数を用いることは誤り
正しくはBland-Altmanプロットを用いる
BlandAltmanLehパッケージでB-Aプロットを描く
- 基本関数のplot( )を使って描く
- ggplot系を使って描くこともできる
タイがあるとき
必要な値を抽出する
おわりに
参考資料

検査の性能を評価する視点として、

異なった状態を検査で区別できるか（識別能discrimination）
反復して測定したときに同じような結果が得られるか（再現性reproducibility*1）

がある。

前者は診断・予測の性能として感度・特異度、ROC曲線などで評価されるもの。
後者はさらに信頼性reliabilityと一致性agreementと区別される。
両方とも測定誤差を評価するものだが、agreementは測定誤差そのものに興味があるのに対し、reliabilityはある集団の中で測定誤差が許容範囲かどうかに興味がある（絶対的か相対的かという話*2 ）。

図1：Agreementとreliabilityの関係. Agreementは同じだが、reliabilityは左の方が高い

Agreementの評価として相関係数を用いることは誤り

同じ対象物を2つの方法で測定したときの観測値がどれくらい一致しているかを評価するときに相関係数（correlation coefficient）を用いてはいけない理由は、

同じものを測るように開発されたのだから関係性があって当たり前
ある程度広がりのあるサンプルが選ばれたら良い相関が得られる
相関係数の解釈の誤解：r=0.1, p=0.01は「P<0.05だから相関がある」ではなく、「r=0.1だから相関がほとんどない」ということが有意に言えるだけ。

正しくはBland-Altmanプロットを用いる

1983年にBlandとAltmanが提唱した方法で、2つの測定値の平均に対して両者の差をプロットする。

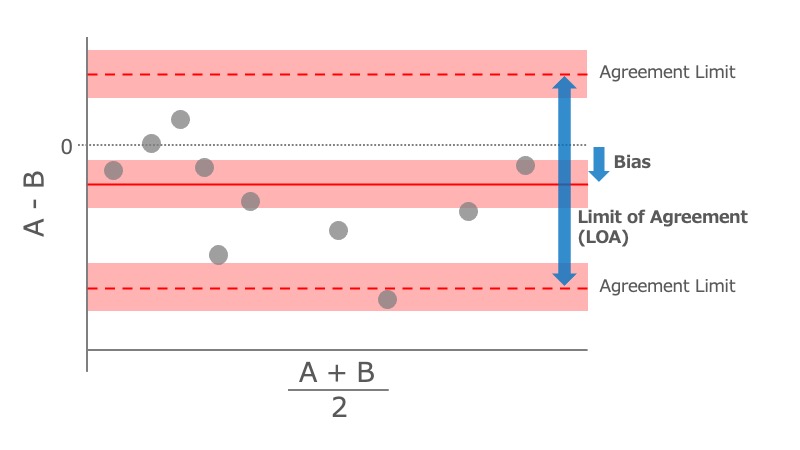
このプロットから次の項目を評価する。

Bias：
Method A, Bが同じように測定できていれば、両者の差d=A-Bは0になるはず。
Mean(d)の0からの偏位をbiasと呼び、全体的な系統的誤差を表している。
dのトレンド：
(A+B)/2が大きくなるにつれてdの変動幅が増加する場合は、差のパーセント $\frac{A-B}{\frac{A+B}{2}}$ を用いるとよい。
回帰直線を重ねて引いてみると傾向がわかりやすいかも。
Limit of agreement（LOA）：
dの標準偏差SD(d)をsとすると、mean(d)±2sの範囲をLOAと呼ぶ。
定義上、dの95%が収まるはずなので、LOAの範囲に全体の95%のプロットが収まっているかを見る。
生物学的妥当性などから、最大でどれくらいのLOAが許容されるのかを事前に決めておく必要あり。
dの正規性：
dが正規分布していることを前提にした分析方法なので、ヒストグラムなどで確認する。

図2の半透明の帯は、それぞれbiasとagreement limitの推定精度を示している。これはサンプルサイズに依存する。
Biasの場合は、

$mean(d) \pm t_{n-1} \sqrt{\frac{s^2}{n}}$

Agreement limitの場合は、

$[mean(d) \pm 2s] \pm t_{n-1} \sqrt{\frac{3s^2}{n}}$

となる。

BlandAltmanLehパッケージでB-Aプロットを描く

以下のサンプルデータを使用する。

library(BlandAltmanLeh)
A <- c(-0.358, 0.788, 1.23, -0.338, -0.789, -0.255, 0.645, 0.506, 
       0.774, -0.511, -0.517, -0.391, 0.681, -2.037, 2.019, -0.447, 
       0.122, -0.412, 1.273, -2.165)
B <- c(0.121, 1.322, 1.929, -0.339, -0.515, -0.029, 1.322, 0.951, 
       0.799, -0.306, -0.158, 0.144, 1.132, -0.675, 2.534, -0.398, 0.537, 
       0.173, 1.508, -1.955)

基本関数のplot( )を使って描く

指定できる主な引数には次のようなものがある。

conf.int：=0.95とするとbiasおよびagreement limitの95%信頼区間をつける
mode：=1ならd = group1 - group2、=2ならd = group2 -group1を用いる

bland.altman.plot(A, B, xlab="Means", ylab="Differences")

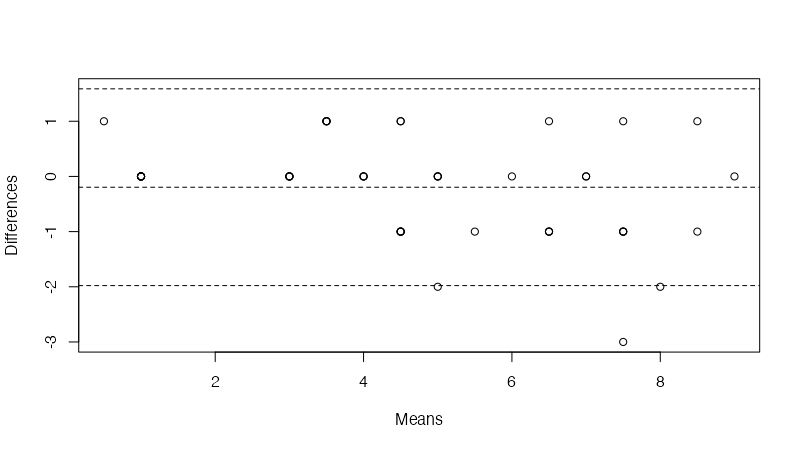
ggplot系を使って描くこともできる

次は95%信頼区間をつけてみる。

library(ggplot2)
q <- bland.altman.plot(A, B, conf.int=0.95, graph.sys = "ggplot2")
print(q)

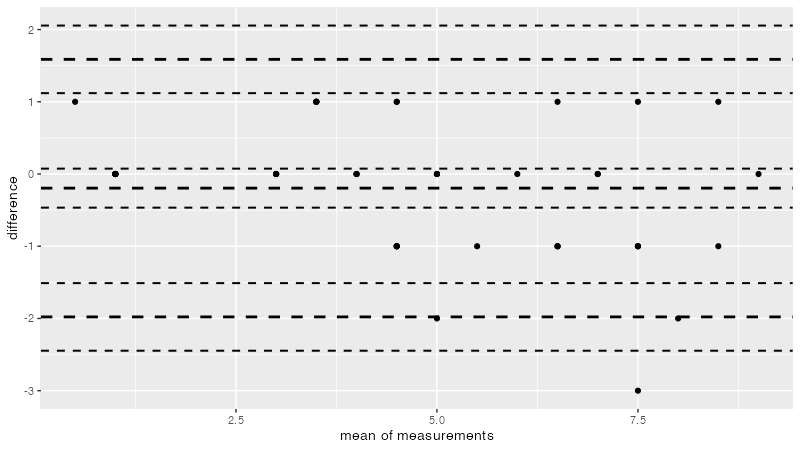
タイがあるとき

同じ箇所にプロットが重なってしまうような場合は工夫が必要。

A <- c(7, 8, 4, 6, 4, 5, 9, 7, 5, 8, 1, 4, 5, 7, 3, 4, 4, 9, 3, 3, 
       1, 4, 5, 6, 4, 7, 4, 7, 7, 5, 4, 6, 3, 4, 6, 4, 7, 4, 6, 5, 1, 1, 1, 1, 1, 1)
B <- c(8, 7, 4, 6, 3, 6, 9, 8, 4, 9, 0, 5, 5, 9, 3, 5, 5, 8, 3, 3, 
       1, 4, 4, 7, 4, 8, 3, 7, 7, 5, 6, 7, 3, 3, 7, 3, 6, 5, 9, 5, 1, 1, 1, 1, 1, 1)

引数sunflower=TRUEとすると、重なりの個数に応じて花弁が増えるプロットにしてくれる（図5）。

bland.altman.plot(A, B, sunflower=TRUE)

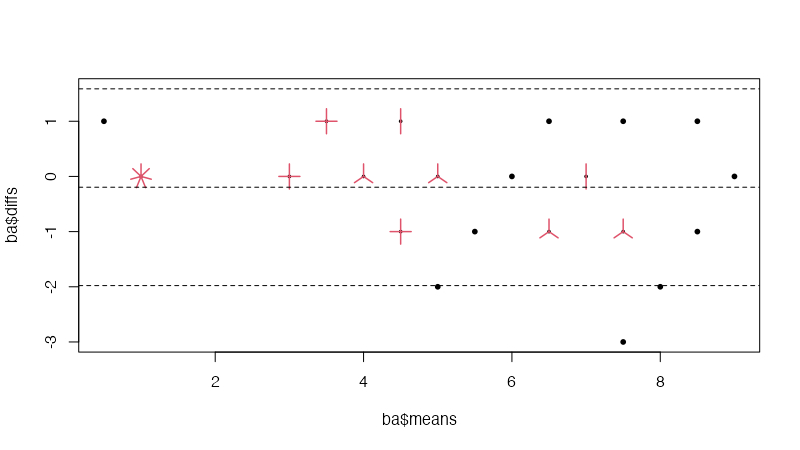
ggplot系であればgeom_count=TRUEとすることでタイの個数に応じてプロットの大きさを変えてくれる。

print(bland.altman.plot(A, B, graph.sys="ggplot2", geom_count=TRUE))

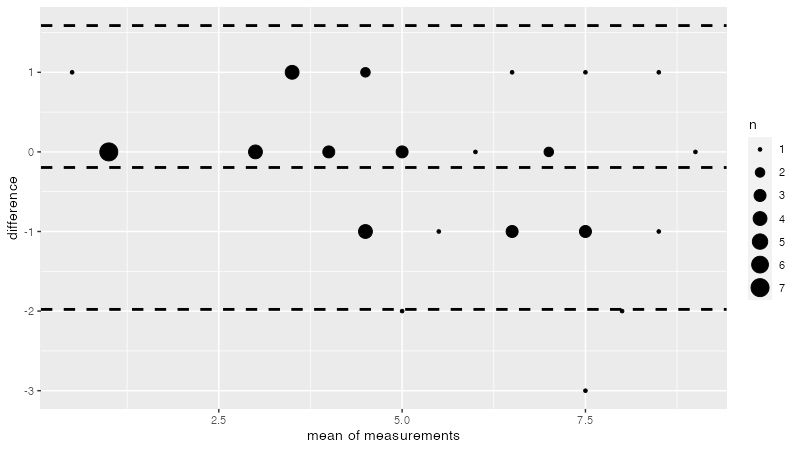
必要な値を抽出する

bland.altman.stats( )を使えばbiasなどの各値を取り出して、自分で描画することも可能。
これを使えばdのヒストグラムも描ける。

> ba.stats <- bland.altman.stats(A, B)
> ba.stats
$means
 [1] -0.1185  1.0550  ...

$diffs
 [1] -0.479 -0.534 ...

$groups
   group1 group2
1  -0.358  0.121
2   0.788  1.322
~~~
20 -2.165 -1.955

$based.on
[1] 20

$lower.limit
[1] -1.009843

$mean.diffs
[1] -0.41395

$upper.limit
[1] 0.1819428

$lines
lower.limit  mean.diffs upper.limit 
 -1.0098428  -0.4139500   0.1819428 

$CI.lines
lower.limit.ci.lower lower.limit.ci.upper   ...
         -1.25629449          -0.76339102         ...

$two
[1] 1.96

$critical.diff
[1] 0.5958928