ねこすたっと

ねこの気持ちと統計について悩む筆者の備忘録的ページ。

回帰モデルの診断・評価(2)：線形性

maths/theory validation R neco

この記事では回帰モデルが満たすべき前提条件のうち、「線形性」について評価する方法について学んでみるつもりです。回帰モデルの満たすべき仮定の概要については以下の記事を参考にしてください。

necostat.hatenablog.jp

線形性（linearity）の仮定とは

線形性とは、

  • f(x_1 + x_2) = f(x_1) + f(x_2)（→ 2つの数値の和を入力したときの出力は、それぞれの値を入力したときの出力の和になる）
  • f(ax) = af(x)（→ 入力をa倍にすると、出力もa倍になる）

という性質のことです。

回帰モデルでは、アウトカムYに対する各説明変数Xの影響が「直線の式」、つまり

\begin{aligned} Y_i &= \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + error \end{aligned}

のようになっていることです。 「直線の式」と表現しましたが、Xの1次式である必要はありません。例えば、

\begin{aligned} Y_i &= \beta_0 + \beta_1 X_{i}^2 + error \\ Y_i &= \beta_0 + \beta_1 \sqrt{X_{i}} + error \\ Y_i &= \beta_0 + \beta_1 \log{X_{i}} + error \\ \end{aligned}

のように、べき乗・平方根・対数のような変換があったとしても、 変換後のXを新しい変数 t_i と置き換えてしまえば、全て下のようになります。

\begin{aligned} Y_i &= \beta_0 + \beta_1 t_i + error \\ \end{aligned}

変換したらOKだったらどんなモデルも線形モデルになりそうですが、下のモデルは非線形モデルです。

\begin{aligned} Y_i &= \beta_0 + X_{i}^{\beta_1} + error \\ \end{aligned}

他にも、加算的であるべき2つの変数の効果に交互作用があると線形性を満たしません。

個人的には説明変数Xに注目するよりも、係数βに注目する*1方が「線形性の仮定」が理解しやすいのではないかと思っています。

Component + Residual Plot（C+R plot）

別名 partial residual plotとも呼ばれます。Partial residual（PR）は次のように定義されます（ここで説明変数は X_1, X_2 の2つだと思ってください）。

\begin{aligned} PR_i &= e_i + \beta_1 X_{1i} \\ \end{aligned}

ここで、 e_i は全ての説明変数を使った線形回帰モデルの残差です。

真の関係性が

\begin{aligned} Y_i &= \alpha_0 + f(X_{1i}) + \alpha_2 X_{2i} + \varepsilon_i \end{aligned}

であるとすると、

\begin{aligned} PR_i &= e_i + \beta_1 X_{1i} \\ &= Y_i - \hat{Y}_i + \beta_1 X_{1i} \\ &= \{\alpha_0 + f(X_{1i}) + \alpha_2 X_{2i} + \varepsilon_i \} - \{\beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i}\} + \beta_1 X_{1i} \\ &= (\alpha_0 - \beta_0) + (\alpha_2 - \beta_2)X_{2i} + f(X_{1i}) + \varepsilon_i \\ &\simeq f(X_{1i}) + \varepsilon_i \end{aligned}

最後の式は \alpha_0 \simeq \beta_0, \alpha_1 \simeq \beta_1 から導かれます。もし X_2 について線形性から大きくかけ離れていたとしても、 \alpha_j と \beta_j はそれほど大きくは違わないだろう、ということだそうです（多分）。

変数 X_1 に対して PR_iをプロットしたものがC+R plotで、 X_1 について線形性が成り立っていればプロットは直線になります。

crPlots( )を使ってC+R plotを描く

まず、irisデータで線形回帰モデルを当てはめます。

fit <- lm(Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width,
          data = iris)

carパッケージを読み込んで、当てはめたモデルをcrPlots( )に渡します。

library(car)
crPlots(fit)

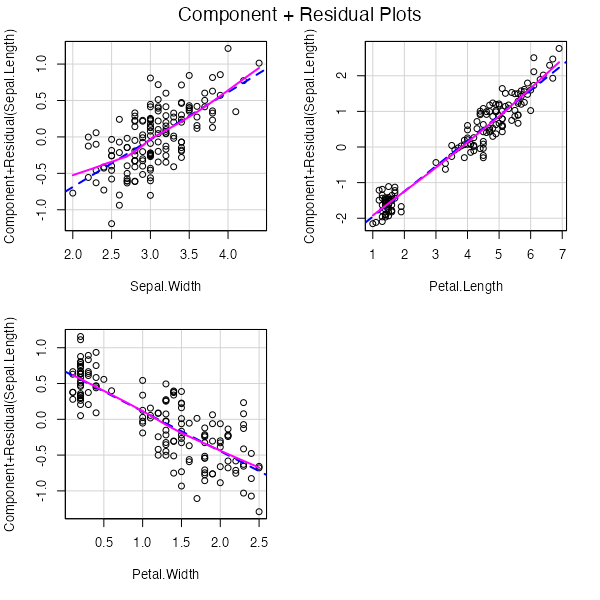
青い点線がそれぞれの変数の係数βを傾きとした直線、ピンクの実線が実際のプロットを局所回帰した曲線です。プロットを見ると、いずれの変数に対しても線形性が仮定できそうです。

Added-Variable Plot（AV plot）

Partial regression plotとも呼ばれるようです。変数 X_1 についてのAV plotは、次の2つをx軸, y軸にとってプロットしたものです。

  • y軸：アウトカム Y を X_1 を除いた変数で回帰したときの残差 e(Y | X_2)
  • x軸：説明変数 X_1 を X_1 を除いた変数で回帰したときの残差 e(X_1 | X_2)

このプロットの傾きが0（= 水平）であれば、「他の変数が含まれている状態では変数 X_1 によって追加される情報はない」ということになります。プロットの様子（曲がり具合）からどのように変数変換したらいいかを判断することに使いたくなりますが、あくまで「この変数を追加して意味があるか」が分かるだけで、線形性については判断できないとのこと。（なので厳密には線形性の評価方法とは言えないようです。）

avPlots( )を使ってAV plotを描く

同じくcarパッケージに含まれているavPlots( )に当てはめたモデルを渡します。

avPlots(fit)

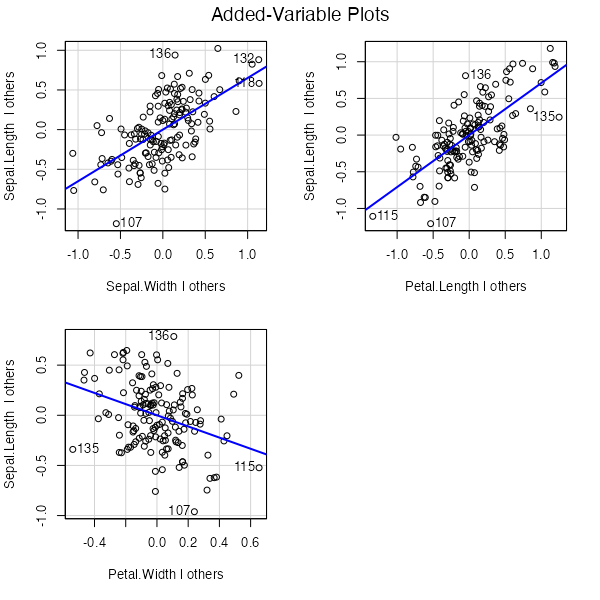
いずれの変数についてもプロットが水平ではないので、モデルに含めて意味がありそうです。

おわりに

  • GLMにも拡張できるそうです。
  • 2匹目の保護猫を迎えてちょうど1年になりました。当初は先住猫と色々あって、本当にお迎えしてよかったのか悩みましたが、そのことも今となってはいい思い出です。

ランキング参加中
統計

参考資料

Applied Linear Statistical Models 5ed (Pb 2013)

Applied Linear Statistical Models 5ed (Pb 2013)

Amazon

  • Applied linear statistical models（5th edition）
    • AV plotについては多く説明されていますが、C+R plotは参考文献を参照という記載のみでした。
  • Regression Graphics: Added-Variable and Component+Residual Plots As Implemented in the car and effects packages for R
    • CANSSI Statistical Software Conference 2022でのレクチャースライドでしょうか。最初に読みました。大変分かりやすかったです。
  • Fox J, Weisberg S. Visualizing Fit and Lack of Fit in Complex Regression Models with Predictor Effect Plots and Partial Residuals. J. Stat. Soft. 2018;87(9):1-27.
  • R.Dennis Cook. Exploring Partial Residual Plots, Technometrics. 1993; 35:4, 351-362
    • Partial residual plotについては、まずこれを読むと全体像が見えやすいかもしれません。
  • R.Dennis Cook. Added-variable plots and curvature in linear regression. Technometrics. 1996; 38:3, 275-278

*1:それぞれのβで偏微分したらどうなるか