ねこすたっと

ねこの気持ちと統計について悩む筆者の備忘録的ページ。

2×2表で関連性をみるための正確検定（Exactパッケージ）[R]

testing dichotomous maths/theory R neco

Fisher正確確率検定（Fisher's exact test）

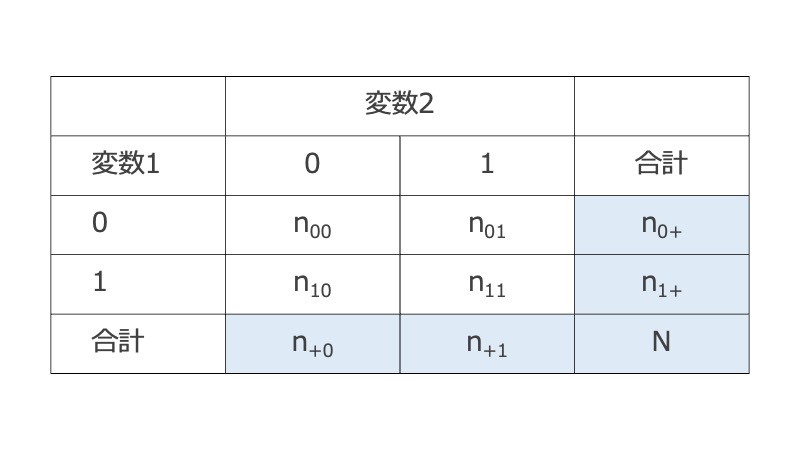
2つの2値変数から作られた2×2表において、全ての周辺度数が与えられた（=固定された）条件下で観察された表よりも極端な値が観察される確率を求め、有意水準α（だいたいは5%）より小さければ「2つの変数間には関連がある」と結論する検定。

ちなみに周辺度数とは、下の表で薄く色が塗られた部分のこと。

2×2表の検定には、このFisher正確確率検定とカイ2乗検定がよく用いられる。 「サンプル数が少ないときはFisher正確確率検定を使え！」はよく言われることで、下のどちらかに当てはまる場合はFisher正確確率検定を使う。

  • 期待度数が 5 以下のマスが全体の 20% 以上ある場合
  • 期待度数が 1 以下のマスが 1 つでもある場合

Fisher正確確率検定の問題点

PCの計算能力が高くなったので、サンプル数が多い場合でもFisher正確確率検定を行うことはできるが問題もある。

過度に保守的：
実際のαエラーが想定している5%を超えることがない（= test sizeが保持される）のは良いが、検出力が低くなりすぎる。

前提条件が満たされる状況ではない：
そもそも全ての周辺度数が固定されている状況は現実的ではない（これについては次で説明追加）。

固定されている周辺度数いろいろ

行も列も固定されているケース

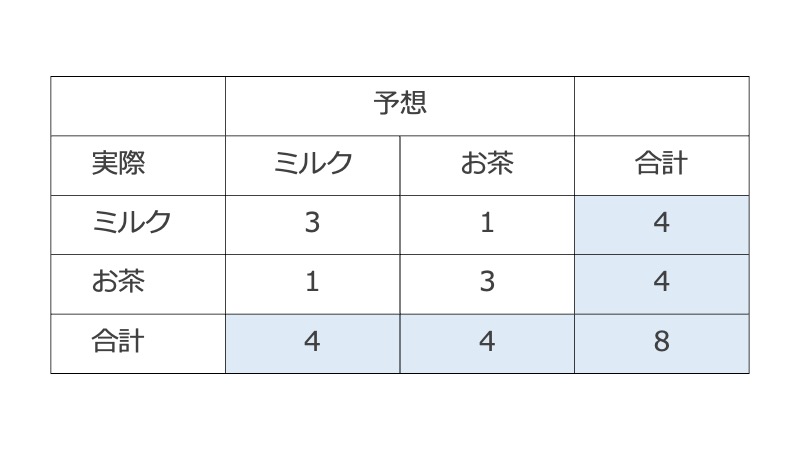
カップにミルクを先に注いで作ったミルクティー4つと、お茶を先に注いで作ったミルクティー4つの合計8杯のミルクティーがランダムに出されて、どちらを先に注いで作られたものかを当てるゲーム（回答者も4つずつであることは知っている）を想定する。

このときは、行の周辺度数も列の周辺度数も最初から分かっているので、Fisher正確確率検定を使う前提条件を満たしている。

実際の臨床研究でこれに相当する状況はほとんど（と言うか、おそらく全く）ない。

このとき、帰無仮説のもとで「ある度数のパターンが観察される確率」は、度数が超幾何分布（hypergeometric distribution）に従うとして計算される（超幾何分布とは何か、Fisher正確確率検定とどう繋がるのか、は詳しく説明してくださってるページがたくさんあります。例えば 超幾何分布 - Wikipediaとか）。

行（あるいは列）のみ固定されているケース

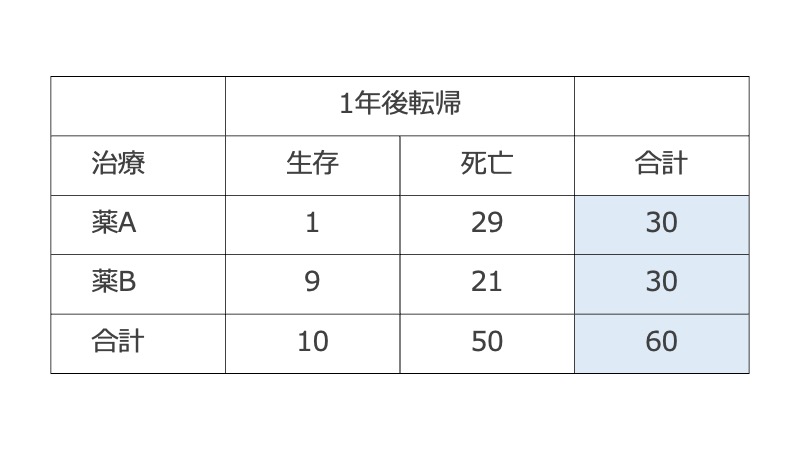
60人の患者を薬A群と薬B群に30人ずつ割り当てて、1年後の転帰（生存/死亡）を調べる状況を想定する。このとき、割り当てる人数は最初から分かっているので行の周辺度数は固定されているが、転帰については何人生存するか最初の時点で分からないので、列の周辺度数は固定されていない。

上の例のような「2つの群でアウトカムの発生確率が等しいかどうか」を見たい介入試験や、「2つの群で過去の要因への曝露確率が等しいかどうか」ケースコントロール研究はこの状況に該当すると考えられる。

このとき、帰無仮説のもとで「ある度数のパターンが観察される確率」は、「同じ発生確率をパラメータに持つ2つの独立した二項分布（binoimal distribution）から求められる確率の積」として計算される。具体的には、

  1. 表の度数が観察される確率は下の2つの確率の積：
    ・薬A群について：生存確率 \pi_A で30回抽出して1回生存が出る確率
    ・薬B群について：生存確率 \pi_B で30回抽出して9回生存が出る確率
  2. 上記と同様の方法で全てのパターンについて確率を計算。
  3. 観察された度数の得られる確率よりも小さいものを全て足し合わせる→（＊）
  4. 帰無仮説のもとでは \pi_A = \pi_B だが、 \pi の値は分からないので、αエラーを超えないために、0から1の \pi のときに与えられる(＊)の最大値をP値とする。

\pi が分からないので計算は大変。この \pi をnuisance parameter（特定されないパラメータ）と呼ぶ。

合計数のみ固定されているケース

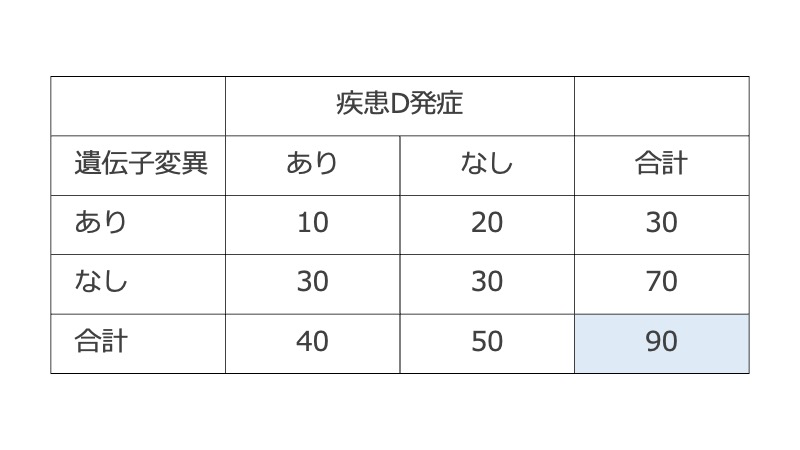
90人の参加者において、遺伝子変異の有無と疾患D発症の有無を横断的に調査する状況を想定する。この場合は、遺伝子変異・疾患D発症のいずれについても最初の時点では分かっていない（それぞれ何人ずつになるのか分からない）。固定されているのは全体数のみ。

このとき、帰無仮説のもとで「ある度数のパターンが観察される確率」は、度数が4つの要素をもった多項分布（multinoimal distribution）に従うとして計算される。帰無仮説のもとでは、多項分布の4つの確率パラメータは、2つの周辺分布の確率パラメータを使って、次のように表せると仮定される。

\begin{aligned} \pi_{00} &= \pi_{0+}\pi_{+0} \\ \pi_{01} &= \pi_{0+}(1-\pi_{+0} \\ \pi_{10} &= (1-\pi_{0+})\pi_{+0} \\ \pi_{11} &= (1-\pi_{0+})(1-\pi_{+0}) \\ \end{aligned}

行（あるいは列）のみ固定されているときよりも分からないパラメータが1つ増えているので余計に計算が大変。

Fisher正確確率検定の過剰な保守性に対処する方法

Fisher正確確率検定（行と列の両方を固定しているのでconditional exact testと呼ぶことも。反対に少なくともどちらかの周辺度数は固定していないものをunconditional exact testと呼ぶ。）の必要以上に過剰な保守性に対処する方法は以下の3つがある。

漸近的アプローチ：

  • カイ2乗検定や尤度比検定など
  • ただしサンプル数が少ないときはダメ、絶対。
  • Yatesの補正（Yates' correction）も使ったらダメ。

mid-P値アプローチ：

  • Fisher検定で求めたP値に、観察された度数が得られる確率の1/2を足す方法
  • 実際のαエラーが想定を超える可能性がある（が、実際は問題になるほどではない）
  • "Quasi-exact"な方法と呼ばれることもあるとのこと

unconditional test：

  • 不必要に周辺度数で条件付けするのがダメなのだから、前述の説明どおり、デザインに応じて必要な周辺度数だけ固定する方法
  • 前提条件まで含めて「正確な（=理想的なαエラーに近い）方法」と言える
  • でも計算負荷がめちゃくちゃ高い。

結局どうすればいいの？

参考資料のRecommended tests for association in 2×2 tablesでは、

In practice, this means that an exact unconditional test is ideal. Pearson’s chi-squared (zpooled) statistic or Fisher–Boschloo’s statistic works well with an exact unconditional test.

と書かれているので、後述のexact.test( )で "Z-pooled" か "Boschloo" を使ったunconditional testをするのが良いのかな。mid-Pアプローチも悪くないし、サンプル数が十分あればPearsonのカイ2乗検定がよいとのこと（ただしYatesの補正は使わない）。そして、Fisher正確確率検定は絶対に使うなよ！と言われている。

今後の自分の方針をどうしようかと思ったとき、下の記事の「それぞれの立場でそれぞれ一理ある」というまとめ方が納得でした。

r-statistics-fan.hatenablog.com

結局のところ、

  • サンプル数が十分ならPearsonのカイ2乗検定を使う
  • サンプル数が少ないときは「周辺度数が全て固定される状況じゃないから過剰に保守的になっているんだよな〜」と思いながら、αエラーが想定を超えてしまわないことを優先してFisher正確確率検定を使う

「小サンプルであってもFisher正確確率検定を使うな」みたいな御達しが出るまでは、上の方針としたいと思っています。

Exactパッケージを使ってunconditional exact testを行う

パッケージを読み込んで、サンプルデータを作成する。

library(Exact)
data <- matrix(c(7, 8, 12, 3), 2, 2, byrow = TRUE) 

> data
     [,1] [,2]
[1,]    7    8
[2,]   12    3

これをexact.test( )に渡す。

exact.test(data, 
           alternative="two.sided", 
           model = "Binomial",
           cond.row = TRUE,
           method = "z-pooled",
           npNumbers = 200)

用いる手法は引数methodで指定できる。

  • "z-pooled"：Z統計量を用いる方法。多分SuissaとShusterの提唱したもの？*1
  • "z-unpooled"：上記のunpooled varianceを使うバージョン（多分）。
  • "santner and snell"：割合の差を使うらしい*2
  • "boschloo"：Boschloo検定。Fisher検定のP値を用いる。
  • "csm"：Barnard CSM検定（CSM=convexity, symmetry, and minimization）。Barnard先生が提案した原法。計算負荷高い。model="Binomial"（後述）のときだけ使える。

"Z-pool"を使ってやってみる。method以外に使うかもしれない引数は次のとおり。

  • model：行もしくは列の周辺度数だけ固定されているなら"Binomial"、合計度数だけ固定されているなら"Multinomial"を指定。
  • cond.row：どちらの周辺度数を固定するか。デフォルトは=TRUEで、行（つまり右端の列）を固定。model="Binomial"のときだけ指定可。
  • npNumbers：npはnuisance parameterの略。Nuisance parameterを変化させて、1番高いP値を有意水準と比べるので、何個試すか、ということ（多分）。デフォルトは100。

出力結果は下。

 Z-pooled Exact Test

data:  7 out of 15 vs. 12 out of 15
test statistic = -1.8943, first sample size = 15, second sample size = 15,
p-value = 0.06822
alternative hypothesis: true difference in proportion is not equal to 0
sample estimates:
difference in proportion 
              -0.3333333

Nuisance parameterの関数としてのP値がグラフで与えられる。赤点が最大となっているところ。

おわりに

  • mid-P exact testは別のexact2x2パッケージで出来そうだったけど、参考文献がだいぶ違ったのでとりあえずまた今度に...。
  • ホットカーペットは猫も人間もダメにします。

ランキング参加中
統計

参考資料

  • 2×2表で関連をみる検定方法の総説。全体像が見えるような構成だったのでとても分かりやすかった。

pubmed.ncbi.nlm.nih.gov

*1:Suissa, Samy, and Jonathan J. Shuster. “Exact Unconditional Sample Sizes for the 2 × 2 Binomial Trial.” Journal of the Royal Statistical Society. Series A (General), vol. 148, no. 4, 1985, pp. 317–27. JSTOR, https://doi.org/10.2307/2981892. Accessed 26 Oct. 2022.

*2:Santner, Thomas J., and Mark K. Snell. “Small-Sample Confidence Intervals for p1 - p2 and p1/p2 in 2 × 2 Contingency Tables.” Journal of the American Statistical Association, vol. 75, no. 370, 1980, pp. 386–94. JSTOR, https://doi.org/10.2307/2287464. Accessed 26 Oct. 2022.