ある点を境にしてアウトカムの変化が急激になっているように見えて、 「変化点はどこなのか」あるいはそもそも「変化点があると言えるのか」を知りたいときがあると思います。
僕もそういうときがあったので少し調べてみました。
使用するパッケージとデータを準備する
segmentedパッケージのdownデータを使います。
library(segmented) data(down)
このデータは母体年齢と出生児のダウン症(21トリソミー)の発生の関連を示したデータで、以下の3つの変数を含みます。
age:母体の平均年齢births:出生数cases:ダウン症を有する児の数
実際のデータはこんな感じ。
> head(down) age births cases 1 17.0 13555 16 2 18.5 13675 15 3 19.5 18752 16 4 20.5 22005 22 5 21.5 23896 16 6 22.5 24667 12
ダウン症発生割合(=cases/births)が母体年齢とどういう関係にあるかを調べるために、まずはプロットしてみます。
library(tidyverse) ggplot(aes(x=age, y=cases/births), data=down) + geom_point(colour="navy", alpha=0.5) + theme_bw()
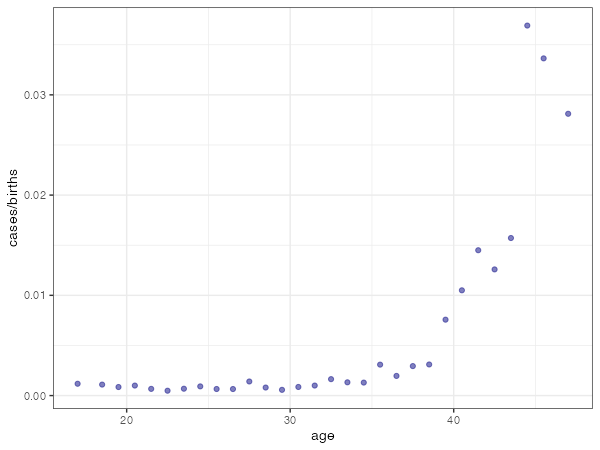
30歳代後半から頻度増加が顕著になっているように見えます。
実際にはcases/birthsのロジットをageで線形回帰しているので、y軸をlogit(cases/births)にしておきましょう。ロジット変換するにはqlogis( )を使います(逆にロジスティック変換するにはplogis( )を使います)。後で使うのでqという名前で保持しておきます。
q <- ggplot(aes(x=age, y=qlogis(cases/births)), data=down) + geom_point(colour="navy", alpha=0.5) + ylab("logit(cases/births)") + theme_bw() print(q)

こうすると30歳までは緩やかに減少して、30歳代前半から増加しているように見えますね。
まずは普通にGLMを当てはめる
まずは普通にglm( )で二項-ロジットモデルを当てはめます。
fit <- glm(cases/births ~ age, weight = births, family = binomial(link=logit), data = down)
> summary(fit) Call: glm(formula = cases/births ~ age, family = binomial(link = "logit"), data = down, weights = births) Deviance Residuals: Min 1Q Median 3Q Max -3.412 -1.943 0.546 2.140 4.767 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -10.562280 0.214342 -49.28 <2e-16 *** age 0.137524 0.006469 21.26 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 625.21 on 29 degrees of freedom Residual deviance: 183.86 on 28 degrees of freedom AIC: 326.74 Number of Fisher Scoring iterations: 5
この書き方が見慣れない方(私もそうでした)は次の記事を参照のこと。
先ほど作図したプロットqに、当てはめられた直線*1を重ねてみます。
q + geom_abline(intercept = fit$coefficients[1], slope = fit$coefficients[2], colour = "indianred1", lwd = 1)
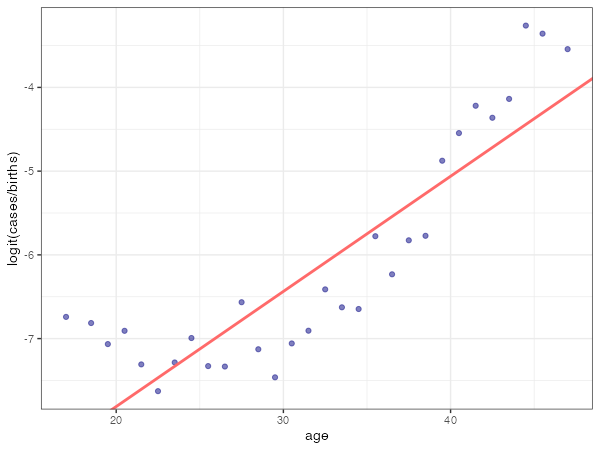
見るからに当てはまってないですね。
segmented modelとは
ここでは下の数式で表されるモデルを当てはめます。
ここで は変化点(breakpoint)、
は年齢が変化点よりも大きいときは1を、大きくないときは0を返す関数です。係数
は、傾きの変化量(difference-in-slope)を表していて、年齢が変化点の手前のときは傾きが
、変化点よりも大きいときの傾きは
になるように推定されます。
Muggeo VM (2008) に推定方法について色々書かれていました。私が押さえ(られ)たのは次の2点です。
- 変化点においては2つの直線間の距離(gap)が0になるはず。このgapが小さくなるように変化点を探していく。
- 変化点があるということは、係数
が0ではないということ。帰無仮説
が棄却されなかったら、そこは統計学的に有意な変化点がないと判断するということ。
変化点は必ずしも1つとは限りませんし、複数の変数について探索することも可能です。
segmented( )で変化点を探す
segmentedパッケージのsegmented( )で変化点を探す方法は意外に簡単でした。さっき当てはめたモデル(のオブジェクト)をsegmented( )に渡すだけです。
指定する代表的な引数は以下のとおり。
seg.Z:変化点を探したい変数名を~xのようにして指定する。複数指定したいときは~x+yのように追加する。psi:変化点を探索する際の初期値
説明変数が1つしかなければseg.Zは明示しなくてもいいですし、初期値psiも必須ではありません。
fit.seg <- segmented(fit, seg.Z = ~age, psi = 35)
結果はsummary( )で取り出します。
> summary(fit.seg) ***Regression Model with Segmented Relationship(s)*** Call: segmented.glm(obj = fit) Estimated Break-Point(s): Est. St.Err psi1.age 31.081 0.724 Meaningful coefficients of the linear terms: Estimate Std. Error z value Pr(>|z|) (Intercept) -6.78244 0.43141 -15.722 <2e-16 *** age -0.01341 0.01795 -0.747 0.455 U1.age 0.27422 0.02324 11.800 NA --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 625.210 on 29 degrees of freedom Residual deviance: 43.939 on 26 degrees of freedom AIC: 190.82 Boot restarting based on 6 samples. Last fit: Convergence attained in 5 iterations (rel. change 4.1199e-11)
変化点
Estimated Break-Point(s)の後には、検出された変化点とその推定誤差が書かれています。このデータだと31歳で傾きが変わっているようです。
confint.segmented( )で変化点の信頼区間を表示することができます。
> confint.segmented(fit.seg) Est. CI(95%).low CI(95%).up psi1.age 31.0811 29.5925 32.5698
傾き
Meaningful coefficients of the linear termsのところには、当てはめられた直線の切片・傾きが書かれています。ageは変化点の前、U1.ageは変化点の後で傾きがどれくらい変化したか、を表しています。つまり先程の式で、,
ということです。
変化点でつながる2つの直線の切片・傾きは、intercept( ), slope( )で得ることができます。手書きで作図したいときはこれらを使います。
> intercept(fit.seg) $age Est. intercept1 -6.7824 intercept2 -15.3060
> slope(fit.seg) $age Est. St.Err. t value CI(95%).l CI(95%).u slope1 -0.01341 0.017947 -0.74722 -0.048586 0.021765 slope2 0.26081 0.014764 17.66500 0.231870 0.289750
slope2は となっていることを確認しました。
Davies検定
先程の結果サマリーで、U1.ageのP値は出ていませんでした。
U1.ageの係数 が有意に0と異なるか、つまり変化点があるかどうかを検定する方法がDavies検定(Davies' test)です。Muggeo VM (2008) によると、K個の変化点を設定したときに計算される統計量をもとに検定するようです。davies.test( )のエラーメッセージによるとKは10以上が推奨と出ますが、Muggeo VM (2008)ではKは5-10程度で十分と書かれています。
davies.test(fit, seg.Z=~age, k=10)
出力結果は以下のとおりです。
Davies' test for a change in the slope data: formula = cases/births ~ age , method = glm model = binomial , link = logit , statist = lrt segmented variable = age 'best' at = 30.5, n.points = 10, p-value < 2.2e-16 alternative hypothesis: two.sided
p-value < 2.2e-16なので統計学的に有意な変化点があって、最良な点は30.5歳という結果でした。Kをめちゃくちゃ大きくすると、前述の推定値31.08に近くなっていくようです。
作図
推定したsegmented modelをグラフにしてみます。fit.segをplot( )に渡したら何となく描いてくれますが、以下の引数を知っておくと良さそうです。
conf.level:信頼区間の幅shade:信頼区間の帯をつけるかどうかlink:リンク関数のスケールで描くかどうか。デフォルトはTRUEなので、前述の例で言うとy軸がロジット変換されたものになっている。
その他に線幅・線色など指定可能。
変化点に関しては、points( )で点推定値を、lines( )で信頼区間を追加することができるみたいです。
plot(fit.seg, conf.level=0.95, shade=TRUE, link=FALSE, lwd=2,col="red") points(fit.seg, link=FALSE, pch=5,col="darkgreen") lines(fit.seg, lwd=2,col="blue")
指定できる引数は、?plot.segmented, ?point.segmented, ?lines.segmentedで見ることができます。points( )ではlinkを指定しますが、lines( )では指定できません。
前述のコードの出力は次のとおり。

おわりに
- 混合効果モデルはnlmeパッケージのlme( )には対応しているようですが、lme4パッケージには対応していないようです(多分)。glmer( )で当てはめた一般線形モデルでsegmented regressionができるといいんですが...
参考資料
- Muggeo VM (2008). “segmented: an R Package to Fit Regression Models with Broken-Line Relationships.” R News, 8(1), 20–25. https://cran.r-project.org/doc/Rnews/.
*1:y軸がロジット変換されているため
![Statistical Methods In Medical Research, 4Ed [Paperback] [Jan 01, 2017] Armitage P. Statistical Methods In Medical Research, 4Ed [Paperback] [Jan 01, 2017] Armitage P.](https://m.media-amazon.com/images/I/41kQ8DLXpPL._SL500_.jpg)